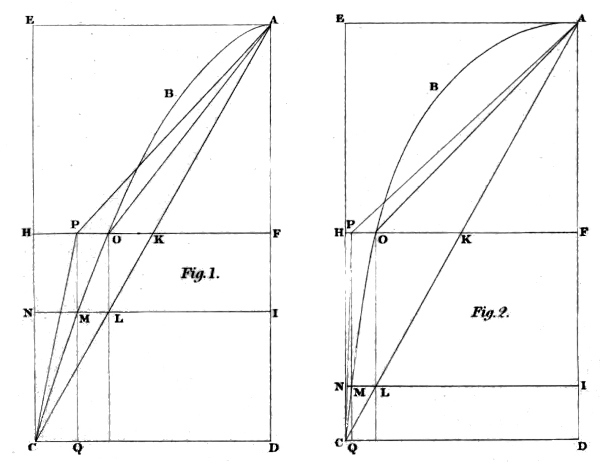
1. A parabola being given, to find a strait line equal to the crooked line of the semiparabola.

Let the parabolical line given be A B C (in figure 1), and the diameter found be A D, and the base drawn D C; and the parallelogram A D C E being completed, draw the strait line A C. Then dividing A D into two equal parts in F, draw F H equal and parallel to D C, cutting A C in K, and the parabolical line in O; and between F H and F O take a mean proportional F P, and draw A O, A P and P C. I say that the two lines A P and P C, taken together as one line, are equal to the parabolical line A B O C.

For the line A B O C being a parabolical line, is generated by the concourse of two motions, one uniform from A to E, the other in the same time uniformly accelerated from rest in A to D. And because the motion from A to E is uniform, A E may represent the times of both those motions from the beginning to the end. Let therefore A E be the time; and consequently the lines ordinately applied in the semiparabola will design the parts of time wherein the body, that describeth the line A B O C, is in every point of the same; so that as at the end of the time A E or D C it is in C, so at the end of the time F O it will be in O. And because the velocity in A D is increased uniformly, that is, in the same proportion with the time, the same lines ordinately applied in the semiparabola will design also the continual augmentation of the impetus, till it be at the greatest, designed by the base D C. Therefore supposing uniform motion in the line A F, in the time F K the body in A by the concourse of the two uniform motions in A F and F K will be moved uniformly in the line A K; and K O will be the increase of the impetus or swiftness gained in the time F K; and the line A O will be uniformly described by the concourse of the two uniform motions in A F and F O in the time F O. From O draw O L parallel to E C, cutting A C in L; and draw L N parallel to D C, cutting E C in N, and the parabolical line in M; and produce it on the other side to A D in I; and I N, I M and I L will be, by the construction of a parabola, in continual proportion, and equal to the three lines F H, F P and F O; and a strait line parallel to E C passing through M will fall on P; and therefore O P will be the increase of impetus gained in the time F O or I L. Lastly, produce P M to C D in Q; and Q C or M N or P H will be the increase of impetus proportional to the time F P or I M or D Q. Suppose now uniform motion from H to C in the time P H. Seeing therefore in the time F P with uniform motion and the impetus increased in proportion to the times, is described the straight line A P; and in the rest of the time and impetus, namely, P H, is described the line C P uniformly; it followeth that the whole line A P C is described with the whole impetus, and in the same time wherewith is described the parabolical line A B C; and therefore the line A P C, made of the two strait lines A P and P C, is equal to the parabolical line A B C; which was to be proved.

2. To find a strait line equal to the crooked line of the first semiparabolaster.

Let A B C be the crooked line of the first semiparabolaster; A D the diameter; D C the base; and let the parallelogram completed be A D C E, whose diagonal is A C. Divide the diameter into two equal parts in F, and draw F H equal and parallel to D C, cutting A C in K, the crooked line in O, and E C in H. Then draw O L parallel to E C, cutting A C in L; and draw L N parallel to the base D C, cutting the crooked line in M, and the strait line E C in N; and produce it on the other side to A D in I. Lastly, through the point M draw P M Q parallel and equal to H C, cutting F H in P; and join C P, A P and A O. I say, the two strait lines A P and P C are equal to the crooked line A B O C.

For the line A B O C, being the crooked line of the first semiparabolaster, is generated by the concourse of two motions, one uniform from A to E, the other in the same time accelerated from rest in A to D, so as that the impetus increaseth in proportion perpetually triplicate to that of the increase of the time, or which is all one, the lengths transmitted are in proportion triplicate to that of the times of their transmission; for as the impetus or quicknesses increase, so the lengths transmitted increase also. And because the motion from A to E is uniform, the line A E may serve to represent the time, and consequently the lines, ordinately drawn in the semiparabolaster, will design the parts of time wherein the body, beginning from rest in A, describeth by its motion the crooked line A B O C. And because D C, which represents the greatest acquired impetus, is equal to A E, the same ordinate lines will represent the several augmentations of the impetus increasing from rest in A. Therefore, supposing uniform motion from A to F, in the time F K there will be described, by the concourse of the two uniform motions A F and F K, the line A K uniformly, and K O will be the increase of impetus in the time F K; and by the concourse of the two uniform motions in A F and F O will be described the line A O uniformly. Through the point L draw the strait line L M N parallel to D C, cutting the strait line A D in I, the crooked line A B C in M, and the strait line E C in N; and through the point M the strait line P M Q parallel and equal to H C, cutting D C in Q and F H in P. By the concourse therefore of the two uniform motions in A F and F P in the time F P will be uniformly described the strait line A P; and L M or O P will be the increase of impetus to be added for the time F O. And because the proportion of I N to I L is triplicate to the proportion of I N to I M, the proportion of F H to F O will also be triplicate to the proportion of F H to F P; and the proportional impetus gained in the time F P is P H. So that F H being equal to D C, which designed the whole impetus acquired by the acceleration, there is no more increase of impetus to be computed. Now in the time P H suppose an uniform motion from H to C; and by the two uniform motions in C H and H P will be described uniformly the strait line P C. Seeing therefore the two strait lines A P and P C are described in the time A E with the same increase of impetus, wherewith the crooked line A B O C is described in the same time A E, that is, seeing the line A P C and the line A B O C are transmitted by the same body in the same time and with equal velocities, the lines themselves are equal; which was to be demonstrated.

By the same method (if any of the semiparabolasters in the table of art. 3 of the precedent chapter be exhibited) may be found a strait line equal to the crooked line thereof, namely, by dividing the diameter into two equal parts, and proceeding as before. Yet no man hitherto hath compared any crooked with any strait line, though many geometricians of every age have endeavoured it. But the cause, why they have not done it, may be this, that there being in Euclid no definition of equality, nor any mark by which to judge of it besides congruity (which is the 8th axiom of the first Book of his Elements) a thing of no use at all in the comparing of strait and crooked; and others after Euclid (except Archimedes and Apollonius, and in our time Bonaventura) thinking the industry of the ancients had reached to all that was to be done in geometry, thought also, that all that could be propounded was either to be deduced from what they had written, or else that it was not at all to be done: it was therefore disputed by some of those ancients themselves, whether there might be any equality at all between crooked and strait lines; which question Archimedes, who assumed that some strait line was equal to the circumference of a circle, seems to have despised, as he had reason. And there is a late writer that granteth that between a strait and a crooked line there is equality; but now, says he, since the fall of Adam, without the special assistance of Divine Grace it is not to be found.

Vol. 1. Lat. & Eng.
C. XVIII.
Fig. 1-2

CHAPTER XIX.

OF ANGLES OF INCIDENCE AND REFLECTION,
EQUAL BY SUPPOSITION.

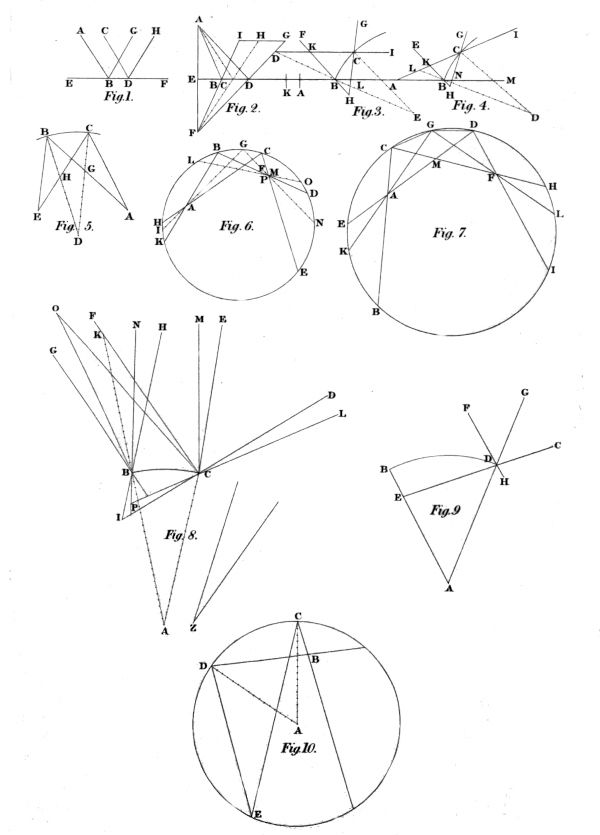
1. If two strait lines falling upon another strait line be parallel, the lines reflected from them shall also be parallel.—2. If two strait lines drawn from one point fall upon another strait line, the lines reflected from them, if they be drawn out the other way, will meet in an angle equal to the angle made by the lines of incidence.—3. If two strait parallel lines, drawn not oppositely, but from the same parts, fall upon the circumference of a circle, the lines reflected from them, if produced they meet within the circle, will make an angle double to that which is made by two strait lines drawn from the centre to the points of incidence.—4. If two strait lines drawn from the same point without a circle fall upon the circumference, and the lines reflected from them being produced meet within the circle, they will make an angle equal to twice that angle, which is made by two strait lines drawn from the centre to the points of incidence, together with the angle which the incident lines themselves make.—5. If two strait lines drawn from one point fall upon the concave circumference of a circle, and the angle they make be less than twice the angle at the centre, the lines reflected from them and meeting within the circle will make an angle, which being added to the angle of the incident lines will be equal to twice the angle at the centre.—6. If through any one point two unequal chords be drawn cutting one another, and the centre of the circle be not placed between them, and the lines reflected from them concur wheresoever, there cannot through the point, through which the two former lines were drawn, be drawn any other strait line whose reflected line shall pass through the common point of the two former lines reflected.—7. In equal chords the same is not true.—8. Two points being given in the circumference of a circle, to draw two strait lines to them, so that their reflected lines may contain any angle given.—9. If a strait line falling upon the circumference of a circle be produced till it reach the semidiameter, and that part of it, which is intercepted between the circumference and the semidiameter, be equal to that part of the semidiameter which is between the point of concourse and the centre, the reflected line will be parallel to the semidiameter.—10. If from a point within a circle, two strait lines be drawn to the circumference, and their reflected lines meet in the circumference of the same circle, the angle made by the reflected lines will be a third part of the angle made by the incident lines.

Whether a body falling upon the superficies of another body and being reflected from it, do make equal angles at that superficies, it belongs not to this place to dispute, being a knowledge which depends upon the natural causes of reflection; of which hitherto nothing has been said, but shall be spoken of hereafter.

In this place, therefore, let it be supposed that the angle of incidence is equal to the angle of reflection; that our present search may be applied, not to the finding out of the causes, but some consequences of the same.

I call an angle of incidence, that which is made between a strait line and another line, strait or crooked, upon which it falls, and which I call the line reflecting; and an angle of reflection equal to it, that which is made at the same point between the strait line which is reflected and the line reflecting.

1. If two strait lines, which fall upon another strait line, be parallel, their reflected lines shall be also parallel.

Let the two strait lines A B and C D (in fig. 1), which fall upon the strait line E F, at the points B and D, be parallel; and let the lines reflected from them be B G and D H. I say, B G and D H are also parallel.

For the angles A B E and C D E are equal by reason of the parallelism of A B and C D; and the angles G B F and H D F are equal to them by supposition; for the lines B G and D H are reflected from the lines A B and C D. Wherefore B G and D H are parallel.

2. If two strait lines drawn from the same point fall upon another strait line, the lines reflected from them, if they be drawn out the other way, will meet in an angle equal to the angle of the incident lines.

From the point A (in fig. 2) let the two strait lines A B and A D be drawn; and let them fall upon the strait line E K at the points B and D; and let the lines B I and D G be reflected from them. I say, I B and G D do converge, and that if they be produced on the other side of the line E K, they shall meet, as in F; and that the angle B F D shall be equal to the angle B A D.

For the angle of reflection I B K is equal to the angle of incidence A B E; and to the angle I B K its vertical angle E B F is equal; and therefore the angle A B E is equal to the angle E B F. Again, the angle A D E is equal to the angle of reflection G D K, that is, to its vertical angle E D F; and therefore the two angles A B D and A D B of the triangle A B D are one by one equal to the two angles F B D and F D B of the triangle F B D; wherefore also the third angle B A D is equal to the third angle B F D; which was to be proved.

Coroll. I. If the strait line A F be drawn, it will be perpendicular to the strait line E K. For both the angles at E will be equal, by reason of the equality of the two angles A B E and F B E, and of the two sides A B and F B.

Coroll. II. If upon any point between B and D there fall a strait line, as A C, whose reflected line is C H, this also produced beyond C, will fall upon F; which is evident by the demonstration above.

3. If from two points taken without a circle, two strait parallel lines, drawn not oppositely, but from the same parts, fall upon the circumference; the lines reflected from them, if produced they meet within the circle, will make an angle double to that which is made by two strait lines drawn from the centre to the points of incidence.

Let the two strait parallels A B and D C (in fig. 3) fall upon the circumference B C at the points B and C; and let the centre of the circle be E; and let A B reflected be B F, and D C reflected be C G; and let the lines F B and G C produced meet within the circle in H; and let E B and E C be connected. I say the angle F H G is double to the angle B E C.

For seeing A B and D C are parallels, and E B cuts A B in B, the same E B produced will cut D C somewhere; let it cut it in D; and let D C be produced howsoever to I, and let the intersection of D C and B F be at K. The angle therefore I C H, being external to the triangle C K H, will be equal to the two opposite angles C K H and C H K. Again, I C E being external to the triangle C D E, is equal to the two angles at D and E. Wherefore the angle I C H, being double to the angle I C E, is equal to the angles at D and E twice taken; and therefore the two angles C K H and C H K are equal to the two angles at D and E twice taken. But the angle C K H is equal to the angles D and A B D, that is, D twice taken; for A B and D C being parallels, the altern angles D and A B D are equal. Wherefore C H K, that is the angle F H G is also equal to the angle at E twice taken; which was to be proved.

Coroll. If from two points taken within a circle two strait parallels fall upon the circumference, the lines reflected from them shall meet in an angle, double to that which is made by two strait lines drawn from the centre to the points of incidence. For the parallels A B and I C falling upon the points B and C, are reflected in the lines B H and C H, and make the angle at H double to the angle at E, as was but now demonstrated.

4. If two strait lines drawn from the same point without a circle fall upon the circumference, and the lines reflected from them being produced meet within the circle, they will make an angle equal to twice that angle, which is made by two strait lines drawn from the centre to the points of incidence, together with the angle which the incident lines themselves make.

Let the two strait lines A B and A C (in fig. 4) be drawn from the point A to the circumference of the circle, whose centre is D; and let the lines reflected from them be B E and C G, and, being produced, make within the circle the angle H; also let the two strait lines D B and D C be drawn from the centre D to the points of incidence B and C. I say, the angle H is equal to twice the angle at D together with the angle at A.

For let A C be produced howsoever to I. Therefore the angle I C H, which is external to the triangle C K H, will be equal to the two angles C K H and C H K. Again, the angle I C D, which is external to the triangle C L D, will be equal to the two angles C L D and C D L. But the angle I C H is double to the angle I C D, and is therefore equal to the angles C L D and C D L twice taken. Wherefore the angles C K H and C H K are equal to the angles C L D and C D L twice taken. But the angle C L D, being external to the triangle A L B, is equal to the two angles L A B and L B A; and consequently C L D twice taken is equal to L A B and L B A twice taken. Wherefore C K H and C H K are equal to the angle C D L together with L A B and L B A twice taken. Also the angle C K H is equal to the angle L A B once and A B K, that is, L B A twice taken. Wherefore the angle C H K is equal to the remaining angle C D L, that is, to the angle at D, twice taken, and the angle L A B, that is, the angle at A, once taken; which was to be proved.

Coroll. If two strait converging lines, as I C and M B, fall upon the concave circumference of a circle, their reflected lines, as C H and B H, will meet in the angle H, equal to twice the angle D, together with the angle at A made by the incident lines produced. Or, if the incident lines be H B and I C, whose reflected lines C H and B M meet in the point N, the angle C N B will be equal to twice the angle D, together with the angle C K H made by the lines of incidence. For the angle C N B is equal to the angle H, that is, to twice the angle D, together with the two angles A, and N B H, that is, K B A. But the angles K B A and A are equal to the angle C K H. Wherefore the angle C N B is equal to twice the angle D, together with the angle C K H made by the lines of incidence I C and H B produced to K.

5. If two strait lines drawn from one point fall upon the concave circumference of a circle, and the angle they make be less than twice the angle at the centre, the lines reflected from them and meeting within the circle will make an angle, which being added to the angle of the incident lines, will be equal to twice the angle at the centre.

Let the two lines A B and A C (in fig. 5), drawn from the point A, fall upon the concave circumference of the circle whose centre is D; and let their reflected lines B E and C E meet in the point E; also let the angle A be less than twice the angle D. I say, the angles A and E together taken are equal to twice the angle D.

For let the strait lines A B and E C cut the strait lines D C and D B in the points G and H; and the angle B H C will be equal to the two angles E B H and E; also the same angle B H C will be equal to the two angles D and D C H; and in like manner the angle B G C will be equal to the two angles A C D and A, and the same angle B G C will be also equal to the two angles D B G and D. Wherefore the four angles E B H, E, A C D and A, are equal to the four angles D, D C H, D B G and D. If, therefore, equals be taken away on both sides, namely, on one side A C D and E B H, and on the other side D C H and D B G, (for the angle E B H is equal to the angle D B G, and the angle A C D equal to the angle D C H), the remainders on both sides will be equal, namely, on one side the angles A and E, and on the other the angle D twice taken. Wherefore the angles A and E are equal to twice the angle D.

Coroll. If the angle A be greater than twice the angle D, their reflected lines will diverge. For, by the corollary of the third proposition, if the angle A be equal to twice the angle D, the reflected lines B E and C E will be parallel; and if it be less, they will concur, as has now been demonstrated. And therefore, if it be greater, the reflected lines B E and C E will diverge, and consequently, if they be produced the other way, they will concur and make an angle equal to the excess of the angle A above twice the angle D; as is evident by art. 4.

6. If through any one point two unequal chords be drawn cutting one another, either within the circle, or, if they be produced, without it, and the centre of the circle be not placed between them, and the lines reflected from them concur wheresoever; there cannot, through the point through which the former lines were drawn, be drawn another strait line, whose reflected line shall pass through the point where the two former reflected lines concur.

Let any two unequal chords, as B K and C H (in fig. 6), be drawn through the point A in the circle B C; and let their reflected lines B D and C E meet in F; and let the centre not be between A B and A C; and from the point A let any other strait line, as A G, be drawn to the circumference between B and C. I say, G N, which passes through the point F, where the reflected lines B D and C E meet, will not be the reflected line of A G.

For let the arch B L be taken equal to the arch B G, and the strait line B M equal to the strait line B A; and L M being drawn, let it be produced to the circumference in O. Seeing therefore B A and B M are equal, and the arch B L equal to the arch B G, and the angle M B L equal to the angle A B G, A G and M L will also be equal, and, producing G A to the circumference in I, the whole lines L O and G I will in like manner be equal. But L O is greater than G F N, as shall presently be demonstrated; and therefore also G I is greater than G N. Wherefore the angles N G C and I G B are not equal. Wherefore the line G F N is not reflected from the line of incidence A G, and consequently no other strait line, besides A B and A C, which is drawn through the point A, and falls upon the circumference B C, can be reflected to the point F; which was to be demonstrated.

It remains that I prove L O to be greater than G N; which I shall do in this manner. L O and G N cut one another in P; and P L is greater than P G. Seeing now L P. P G :: P N. P O are proportionals, therefore the two extremes L P and P O together taken, that is L O, are greater than P G and P N together taken, that is, G N; which remained to be proved.

7. But if two equal chords be drawn through one point within a circle, and the lines reflected from them meet in another point, then another strait line may be drawn between them through the former point, whose reflected line shall pass through the latter point.

Let the two equal chords B C and E D (in the 7th figure) cut one another in the point A within the circle B C D; and let their reflected lines C H and D I meet in the point F. Then dividing the arch C D equally in G, let the two chords G K and G L be drawn through the points A and F. I say, G L will be the line reflected from the chord K G. For the four chords B C, C H, E D and D I are by supposition all equal to one another; and therefore the arch B C H is equal to the arch E D I; as also the angle B C H to the angle E D I; and the angle A M C to its verticle angle F M D; and the strait line D M to the strait line G M; and, in like manner, the strait line A C to the strait line F D; and the chords C G and G D being drawn, will also be equal; and also the angles F D G and A C G, in the equal segments G D I and G C B. Wherefore the strait lines F G and A G are equal; and, therefore, the angle F G D is equal to the angle A G C, that is, the angle of incidence equal to the angle of reflection. Wherefore the line G L is reflected from the incident line C G; which was to be proved.

Coroll. By the very sight of the figure it is manifest, that if G be not the middle point between C and D, the reflected line G L will not pass through the point F.

8. Two points in the circumference of a circle being given to draw two strait lines to them, so as that their reflected lines may be parallel, or contain any angle given.

In the circumference of the circle, whose centre is A, (in the 8th figure) let the two points B and C be given; and let it be required to draw to them from two points taken without the circle two incident lines, so that their reflected lines may, first, be parallel.

Let A B and A C be drawn; as also any incident line D C, with its reflected line C F; and let the angle E C D be made double to the angle A; and let H B be drawn parallel to E C, and produced till it meet with D C produced in I. Lastly, producing A B indefinitely to K, let G B be drawn so that the angle G B K may be equal to the angle H B K, and then G B will be the reflected line of the incident line H B. I say, D C and H B are two incident lines, whose reflected lines C F and B G are parallel.

For seeing the angle E C D is double to the angle B A C, the angle H I C is also, by reason of the parallels E C and H I, double to the same B A C; therefore also F C and G B, namely, the lines reflected from the incident lines D C and H B, are parallel. Wherefore the first thing required is done.

Secondly, let it be required to draw to the points B and C two strait lines of incidence, so that the lines reflected from them may contain the given angle Z.

To the angle E C D made at the point C, let there be added on one side the angle D C L equal to half Z, and on the other side the angle E C M equal to the angle D C L; and let the strait line B N be drawn parallel to the strait line C M; and let the angle K B O be made equal to the angle N B K; which being done, B O will be the line of reflection from the line of incidence N B. Lastly, from the incident line L C, let the reflected line C O be drawn, cutting B O at O, and making the angle C O B. I say, the angle C O B is equal to the angle Z.

Let N B be produced till it meet with the strait line L C produced in P. Seeing, therefore, the angle L C M is, by construction, equal to twice the angle B A C, together with the angle Z; the angle N P L, which is equal to L C M by reason of the parallels N P and M C, will also be equal to twice the same angle B A C, together with the angle Z. And seeing the two strait lines O C and O B fall from the point O upon the points C and B; and their reflected lines L C and N B meet in the point P; the angle N P L will be equal to twice the angle B A C together with the angle C O B. But I have already proved the angle N P L to be equal to twice the angle B A C together with the angle Z. Therefore the angle C O B is equal to the angle Z; wherefore, two points in the circumference of a circle being given, I have drawn, &c.; which was to be done.

But if it be required to draw the incident lines from a point within the circle, so that the lines reflected from them may contain an angle equal to the angle Z, the same method is to be used, saving that in this case the angle Z is not to be added to twice the angle B A C, but to be taken from it.

9. If a strait line, falling upon the circumference of a circle, be produced till it reach the semidiameter, and that part of it which is intercepted between the circumference and the semidiameter be equal to that part of the semidiameter which is between the point of concourse and the centre, the reflected line will be parallel to the semidiameter.

Let any line A B (in the 9th figure) be the semidiameter of the circle whose centre is A; and upon the circumference B D let the strait line C D fall, and be produced till it cut A B in E, so that E D and E A may be equal; and from the incident line C D let the line D F be reflected. I say, A B and D F will be parallel.

Let A G be drawn through the point D. Seeing, therefore, E D and E A are equal, the angles E D A and E A D will also be equal. But the angles F D G and E D A are equal; for each of them is half the angle E D H or F D C. Wherefore the angles F D G and E A D are equal; and consequently D F and A B are parallel; which was to be proved.

Coroll. If E A be greater then E D, then D F and A B being produced will concur; but if E A be less than E D, then B A and D H being produced will concur.

10. If from a point within a circle two strait lines be drawn to the circumference, and their reflected lines meet in the circumference of the same circle, the angle made by the lines of reflection will be a third part of the angle made by the lines of incidence.

From the point B (in the 10th figure) taken within the circle whose centre is A, let the two strait lines B C and B D be drawn to the circumference; and let their reflected lines C E and D E meet in the circumference of the same circle at the point E. I say, the angle C E D will be a third part of the angle C B D.

Let A C and A D be drawn. Seeing, therefore, the angles C E D and C B D together taken are equal to twice the angle C A D (as has been demonstrated in the 5th article); and the angle C A D twice taken is quadruple to the angle C E D; the angles C E D and C B D together taken will also be equal to the angle C E D four times taken; and therefore if the angle C E D be taken away on both sides, there will remain the angle C B D on one side, equal to the angle C E D thrice taken on the other side; which was to be demonstrated.

Coroll. Therefore a point being given within a circle, there may be drawn two lines from it to the circumference, so as their reflected lines may meet in the circumference. For it is but trisecting the angle C B D, which how it may be done shall be shown in the following chapter.

Vol. 1. Lat. & Eng.
C. XIX.
Fig. 1-10

CHAPTER XX.

OF THE DIMENSION OF A CIRCLE, AND THE
DIVISION OF ANGLES OR ARCHES.

1. The dimension of a circle never determined in numbers by Archimedes and others.—2. The first attempt for the finding out of the dimension of a circle by lines.—3. The second attempt for the finding out of the dimension of a circle from the consideration of the nature of crookedness.—4. The third attempt; and some things propounded to be further searched into.—5. The equation of the spiral of Archimedes with a strait line.—6. Of the analysis of geometricians by the powers of lines.

1. In the comparing of an arch of a circle with a strait line, many and great geometricians, even from the most ancient times, have exercised their wits; and more had done the same, if they had not seen their pains, though undertaken for the common good, if not brought to perfection, vilified by those that envy the praises of other men. Amongst those ancient writers whose works are come to our hands, Archimedes was the first that brought the length of the perimeter of a circle within the limits of numbers very little differing from the truth; demonstrating the same to be less than three diameters and a seventh part, but greater than three diameters and ten seventy-one parts of the diameter. So that supposing the radius to consist of 10,000,000 equal parts, the arch of a quadrant will be between 15,714,285 and 15,704,225 of the same parts. In our times, Ludovicus Van Cullen and Willebrordus Snellius, with joint endeavour, have come yet nearer to the truth; and pronounced from true principles, that the arch of a quadrant, putting, as before, 10,000,000 for radius, differs not one whole unity from the number 15,707,963; which, if they had exhibited their arithmetical operations, and no man had discovered any error in that long work of theirs, had been demonstrated by them. This is the furthest progress that has been made by the way of numbers; and they that have proceeded thus far deserve the praise of industry. Nevertheless, if we consider the benefit, which is the scope at which all speculation should aim, the improvement they have made has been little or none. For any ordinary man may much sooner and more accurately find a strait line equal to the perimeter of a circle, and consequently square the circle, by winding a small thread about a given cylinder, than any geometrician shall do the same by dividing the radius into 10,000,000 equal parts. But though the length of the circumference were exactly set out, either by numbers, or mechanically, or only by chance, yet this would contribute no help at all towards the section of angles, unless happily these two problems, to divide a given angle according to any proportion assigned, and to find a strait line equal to the arch of a circle, were reciprocal, and followed one another. Seeing therefore the benefit proceeding from the knowledge of the length of the arch of a quadrant consists in this, that we may thereby divide an angle according to any proportion, either accurately, or at least accurately enough for common use; and seeing this cannot be done by arithmetic, I thought fit to attempt the same by geometry, and in this chapter to make trial whether it might not be performed by the drawing of strait and circular lines.

2. Let the square A B C D (in the first figure) be described; and with the radii A B, B C, and D C, the three arches B D, C A, and A C; of which let the two B D and C A cut one another in E, and the two B D and A C in F. The diagonals therefore B D and A C being drawn will cut one another in the centre of the square G, and the two arches B D and C A in two equal parts in H and Y; and the arch B H D will be trisected in F and E. Through the centre G let the two strait lines K G L and M G N be drawn parallel and equal to the sides of the square A B and A D, cutting the four sides of the same square in the points K, L, M, and N; which being done, K L will pass through F, and M N through E. Then let O P be drawn parallel and equal to the side B C, cutting the arch B F D in F, and the sides A B and D C in O and P. Therefore O F will be the sine of the arch B F, which is an arch of 30 degrees; and the same O F will be equal to half the radius. Lastly, dividing the arch B F in the middle in Q, let R Q, the sine of the arch B Q, be drawn and produced to S, so that Q S be equal to R Q, and consequently R S be equal to the chord of the arch B F; and let F S be drawn and produced to T in the side B C. I say, the strait line B T is equal to the arch B F; and consequently that B V, the triple of B T, is equal to the arch of the quadrant B F E D.

Let T F be produced till it meet the side B A produced in X; and dividing O F in the middle in Z, let Q Z be drawn and produced till it meet with the side B A produced. Seeing therefore the strait lines R S and O F are parallel, and divided in the midst in Q and Z, Q Z produced will fall upon X, and X Z Q produced to the side B C will cut B T in the midst in α.

Upon the strait line F Z, the fourth part of the radius A B, let the equilateral triangle a Z F be constituted; and upon the centre a, with the radius a Z, let the arch Z F be drawn; which arch Z F will therefore be equal to the arch Q F, the half of the arch B F. Again, let the strait line Z O be cut in the midst in b, and the strait line b O in the midst in c; and let the bisection be continued in this manner till the last part O c be the least that can possibly be taken; and upon it, and all the rest of the parts equal to it into which the strait line O F may be cut, let so many equilateral triangles be understood to be constituted; of which let the last be d O c. If, therefore, upon the centre d, with the radius d O, be drawn the arch O c, and upon the rest of the equal parts of the strait line O F be drawn in like manner so many equal arches, all those arches together taken will be equal to the whole arch B F, and the half of them, namely, those that are comprehended between O and Z, or between Z and F, will be equal to the arch B Q or Q F, and in sum, what part soever the strait line O c be of the strait line O F, the same part will the arch O c be of the arch B F, though both the arch and the chord be infinitely bisected. Now seeing the arch O c is more crooked than that part of the arch B F which is equal to it; and seeing also that the more the strait line X c is produced, the more it diverges from the strait line X O, if the points O and c be understood to be moved forwards with strait motion in X O and X c, the arch O c will thereby be extended by little and little, till at the last it come somewhere to have the same crookedness with that part of the arch B F which is equal to it. In like manner, if the strait line X b be drawn, and the point b be understood to be moved forwards at the same time, the arch c b will also by little and little be extended, till its crookedness come to be equal to the crookedness of that part of the arch B F which is equal to it. And the same will happen in all those small equal arches which are described upon so many equal parts of the strait line O F. It is also manifest, that by strait motion in X O and X Z all those small arches will lie in the arch B F, in the points B, Q and F. And though the same small equal arches should not be coincident with the equal parts of the arch B F in all the other points thereof, yet certainly they will constitute two crooked lines, not only equal to the two arches B Q and Q F, and equally crooked, but also having their cavity towards the same parts; which how it should be, unless all those small arches should be coincident with the arch B F in all its points, is not imaginable. They are therefore coincident, and all the strait lines drawn from X, and passing through the points of division of the strait line O F, will also divide the arch B F into the same proportions into which O F is divided.

Now seeing X b cuts off from the point B the fourth part of the arch B F, let that fourth part be B e; and let the sine thereof, f e, be produced to F T in g, for so f e will be the fourth part of the strait line f g, because as O b is to O F, so is f e to f g. But B T is greater than f g; and therefore the same B T is greater than four sines of the fourth part of the arch B F. And in like manner, if the arch B F be subdivided into any number of equal parts whatsoever, it may be proved that the strait line B T is greater than the sine of one of those small arches, so many times taken as there be parts made of the whole arch B F. Wherefore the strait line B T is not less than the arch B F. But neither can it be greater, because if any strait line whatsoever, less than B T, be drawn below B T, parallel to it, and terminated in the strait lines X B and X T, it would cut the arch B F; and so the sine of some one of the parts of the arch B F, taken so often as that small arch is found in the whole arch B F, would be greater than so many of the same arches; which is absurd. Wherefore the strait line B T is equal to the arch B F; and the strait line B V equal to the arch of the quadrant B F D; and B V four times taken, equal to the perimeter of the circle described with the radius A B. Also the arch B F and the strait line B T are everywhere divided into the same proportions; and consequently any given angle, whether greater or less than B A F, may be divided into any proportion given.

But the strait line B V, though its magnitude fall within the terms assigned by Archimedes, is found, if computed by the canon of signs, to be somewhat greater than that which is exhibited by the Rudolphine numbers. Nevertheless, if in the place of B T, another strait line, though never so little less, be substituted, the division of angles is immediately lost, as may by any man be demonstrated by this very scheme.

Howsoever, if any man think this my strait line B V to be too great, yet, seeing the arch and all the parallels are everywhere so exactly divided, and B V comes so near to the truth, I desire he would search out the reason, why, granting B V to be precisely true, the arches cut off should not be equal.

But some man may yet ask the reason why the strait lines, drawn from X through the equal parts of the arch B F, should cut off in the tangent B V so many strait lines equal to them, seeing the connected straight line X V passes not through the point D, but cuts the strait line A D produced in l; and consequently require some determination of this problem. Concerning which, I will say what I think to be the reason, namely, that whilst the magnitude of the arch doth not exceed the magnitude of the radius, that is, the magnitude of the tangent B C, both the arch and the tangent are cut alike by the strait lines drawn from X; otherwise not. For A V being connected, cutting the arch B H D in I, if X C being drawn should cut the same arch in the same point I, it would be as true that the arch B I is equal to the radius B C, as it is true that the arch B F is equal to the strait line B T; and drawing X K it would cut the arch B I in the midst in i; also drawing A i and producing it to the tangent B C in k, the strait line B k will be the tangent of the arch B i, (which arch is equal to half the radius) and the same strait line B k will be equal to the strait line k I. I say all this is true, if the preceding demonstration be true; and consequently the proportional section of the arch and its tangent proceeds hitherto. But it is manifest by the golden rule, that taking B h double to B T, the line X h shall not cut off the arch B E, which is double to the arch B F, but a much greater. For the magnitude of the straight lines X M, X B, and M E, being known (in numbers), the magnitude of the strait line cut off in the tangent by the strait line X E produced to the tangent, may also be known; and it will be found to be less than B h; Wherefore the strait line X h being drawn, will cut off a part of the arch of the quadrant greater than the arch B E. But I shall speak more fully in the next article concerning the magnitude of the arch B I.

And let this be the first attempt for the finding out of the dimension of a circle by the section of the arch B F.