Every Proposition in the Second Book has either a square or a rectangle in its enunciation. Before commencing it the student should read the following preliminary explanations: by their assistance it will be seen that this Book, which is usually considered difficult, will be rendered not only easy, but almost intuitively evident.
1. As the linear unit is that by which we express all linear measures, so the square unit is that to which all superficial measures are referred. Again, as there are different linear units in use, such as in this country, inches, feet, yards, miles, &c., and in France, metres, and their multiples or sub-multiples, so different square units are employed.
2. A square unit is the square described on a line whose length is the linear unit. Thus a square inch is the square described on a line whose length is an inch; a square foot is the square described on a line whose length is a foot, &c.
3. If we take a linear foot, describe a square on it, divide two adjacent sides each into twelve equal parts, and draw parallels to the sides, we evidently divide the square foot into square inches; and as there will manifestly be 12 rectangular parallelograms, each containing 12 square inches, the square foot contains 144 square inches.
In the same manner it can be shown that a square yard contains 9 square feet; and so in general the square described on any line contains n2 times the square described on the nth part of the line. Thus, as a simple case, the square on a line is four times the square on its half. On account of this property the second power of a quantity is called its square; and, conversely, the square on a line AB is expressed symbolically by AB2.
4. If a rectangular parallelogram be such that two adjacent sides contain respectively m and n linear units, by dividing one side into m and the other into n equal parts, and drawing parallels to the sides, the whole area is evidently divided into mn square units. Hence the area of the parallelogram is found by multiplying its length by its breadth, and this explains why we say (see Def. iv.) a rectangle is contained by any two adjacent sides; for if we multiply the length of one by the length of the other we have the area. Thus, if AB, AD be two adjacent sides of a rectangle, the rectangle is expressed by AB.AD.
Definitions.
i. If a point C be taken in a line AB, the parts AC, CB are called segments, and C a point of division.
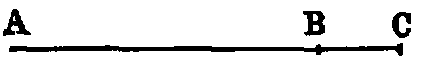
ii. If C be taken in the line AB produced, AC, CB are still called the segments of the line AB; but C is called a point of external division.
iii. A parallelogram whose angles are right angles is called a rectangle.

iv. A rectangle is said to be contained by any two adjacent sides. Thus the rectangle ABCD is said to be contained by AB, AD, or by AB, BC, &c.
v. The rectangle contained by two separate lines such as AB and CD is the parallelogram formed by erecting a perpendicular to AB, at A, equal to CD, and drawing parallels: the area of the rectangle will be AB.CD.
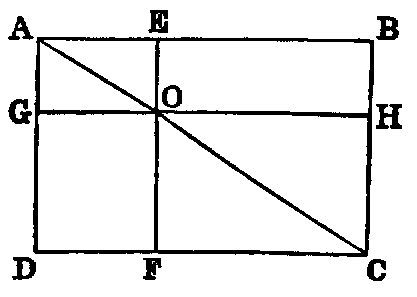
vi. In any parallelogram the figure which is composed of either of the parallelograms about a diagonal and the two complements [see I., xliii.] is called a gnomon. Thus, if we take away either of the parallelograms AO, OC from the parallelogram AC, the remainder is called a gnomon.
PROP. I.—Theorem.
If there be two lines (A, BC), one of which is divided into any number of parts (BD, DE, EC), the rectangle contained by the two lines (A, BC), is equal to the sum of the rectangles contained by the undivided line (A) and the several parts of the divided line.
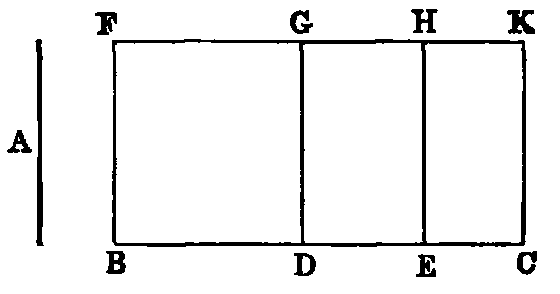
Dem.—Erect BF at right angles to BC [I., xi.] and make it equal to A. Complete the parallelogram BK (Def. v.). Through D, E draw DG, EH parallel to BF. Because the angles at B, D, E are right angles, each of the quadrilaterals BG, DH, EK is a rectangle. Again, since A is equal to BF (const.), the rectangle contained by A and BC is the rectangle contained by BF and BC (Def. v.); but BK is the rectangle contained by BF and BC. Hence the rectangle contained by A and BC is BK. In like manner the rectangle contained by A and BD is BG. Again, since A is equal to BF (const.), and BF is equal to DG [I. xxxiv.], A is equal to DG. Hence the rectangle contained by A and DE is the figure DH (Def. v.). In like manner the rectangle contained by A and EC is the figure EK. Hence we have the following identities:—
| Rectangle | contained | by A | and | BD ≡ BG. |
| ,, | ,, | A | ,, | DE ≡ DH. |
| ,, | ,, | A | ,, | EC ≡ EK. |
| ,, | ,, | A | ,, | BC ≡ BK. |
But BK is equal to the sum of BG, DH, EK (I., Axiom ix.). Therefore the rectangle contained by A and BC is equal to the sum of the rectangles contained by A and BD, A and DE, A and EC.
If we denote the lines BD, DE, EC by a, b, c, the Proposition asserts that the rectangle contained by A, and a + b + c is equal to the sum of the rectangles contained by A and a, A and b, A and c, or, as it may be written, A(a + b + c) = Aa + Ab + Ac. This corresponds to the distributive law in multiplication, and shows that rectangles in Geometry, and products in Arithmetic and Algebra, are subject to the same rules.
Illustration.—Suppose A to be 6 inches; BD, 5 inches; DE, 4 inches; EC, 3 inches; then BC will be 12 inches; and the rectangles will have the following values:—
| Rectangle | A.BC = 6 × 12 = 72 | square inches. |
| ,, | A.BD = 6 × 5 = 30 | ,, |
| ,, | A.DE = 6 × 4 = 24 | ,, |
| ,, | A.EC = 6 × 3 = 18 | ,, |
Now the sum of the three last rectangles, viz. 30, 24, 18, is 72. Hence the rectangle A.BC = A.BD + A.DE + A.EC.
The Second Book is occupied with the relations between the segments of a line divided in various ways. All these can be proved in the most simple manner by Algebraic Multiplication. We recommend the student to make himself acquainted with the proofs by this method as well as with those of Euclid. He will thus better understand the meaning of each Proposition.
Cor. 1.—The rectangle contained by a line and the difference of two others is equal to the difference of the rectangles contained by the line and each of the others.
Cor. 2.—The area of a triangle is equal to half the rectangle contained by its base and perpendicular.
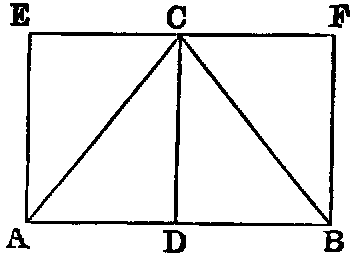
Dem.—From the vertex C let fall the perpendicular CD. Draw EF parallel to
AB, and AE, BF each parallel to CD. Then AF is the rectangle contained by AB
and BF; but BF is equal to CD. Hence AF = AB.CD; but [I. xli.] the
triangle ABC is = half the parallelogram AF. Therefore the triangle ABC is
= 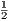 AB.CD.
AB.CD.
PROP. II.—Theorem.
If a line (AB) be divided into any two parts (at C), the square on the whole line is equal to the sum of the rectangles contained by the whole and each of the segments (AC, CB).
Dem.—On AB describe the square ABDF [I. xlvi.], and through C draw CE parallel to AF [I. xxxi.]. Now, since AB is equal to AF, the rectangle contained by AB and AC is equal to the rectangle contained by AF and AC; but AE is the rectangle contained by AF and AC. Hence the rectangle contained by AB and AC is equal to AE. In like manner the rectangle contained by AB and CB is equal to the figure CD. Therefore the sum of the two rectangles AB.AC, AB.CB is equal to the square on AB.
| Or thus: | AB | = AC + CB, | |||||||||
| and | AB | = AB. | |||||||||
| Hence, multiplying, we get | AB2 | = AB.AC + AB.CB. |
This Proposition is the particular case of i. when the divided and undivided lines are equal, hence it does not require a separate Demonstration.
PROP. III.—Theorem.
If a line (AB) be divided into two segments (at C), the rectangle contained by the whole line and either segment (CB) is equal to the square on that segment together with the rectangle contained by the segments.

Dem.—On BC describe the square BCDE [I. xlvi.]. Through A draw AF parallel to CD: produce ED to meet AF in F. Now since CB is equal to CD, the rectangle contained by AC, CB is equal to the rectangle contained by AC, CD; but the rectangle contained by AC, CD is the figure AD. Hence the rectangle AC.CB is equal to the figure AD, and the square on CB is the figure CE. Hence the rectangle AC.CB, together with the square on CB, is equal to the figure AE.
Again, since CB is equal to BE, the rectangle AB.CB is equal to the rectangle AB.BE; but the rectangle AB.BE is equal to the figure AE. Hence the rectangle AB.CB is equal to the figure AE. And since things which are equal to the same are equal to one another, the rectangle AC.CB, together with the square on CB, is equal to the rectangle AB.CB.
| Or thus: | AB | = AC + CB, | |||||||||
| CB | = CB. | ||||||||||
| Hence | AB.CB | = AC.CB + CB2. |
Prop. iii. is the particular case of Prop. i., when the undivided line is equal to a segment of the divided line.
PROP. IV.—Theorem.
If a line (AB) be divided into any two parts (at C), the square on the whole line is equal to the sum of the squares on the parts (AC, CB), together with twice their rectangle.
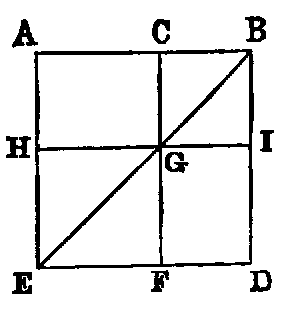
Dem.—On AB describe a square ABDE. Join EB; through C draw CF parallel to AE, intersecting BE in G; and through G draw HI parallel to AB.
Now since AE is equal to AB, the angle ABE is equal to AEB [I. v.]; but since BE intersects the parallels AE, CF, the angle AEB is equal to CGB [I. xxix.]. Hence the angle CBG is equal to CGB, and therefore [I. vi.] CG is equal to CB; but CG is equal to BI and CB to GI. Hence the figure CBIG is a lozenge, and the angle CBI is right. Hence (I., Def. xxx.) it is a square. In like manner the figure EFGH is a square.
Again, since CB is equal to CG, the rectangle AC.CB is equal to the rectangle AC.CG; but AC.CG is the figure AG (Def. iv.). Therefore the rectangle AC.CB is equal to the figure AG. Now the figures AG, GD are equal [I. xliii.], being the complements about the diagonal of the parallelogram AD. Hence the parallelograms AG, GD are together equal to twice the rectangle AC.CB. Again, the figure HF is the square on HG, and HG is equal to AC. Therefore HF is equal to the square on AC, and CI is the square on CB; but the whole figure AD, which is the square on AB, is the sum of the four figures HF, CI, AG, GD. Therefore the square on AB is equal to the sum of the squares on AC, CB, and twice the rectangle AC.CB.
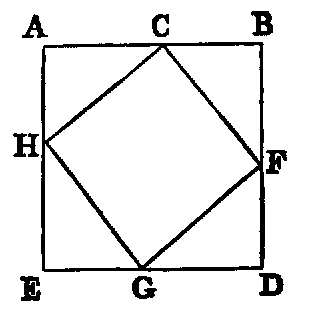
Or thus: On AB describe the square ABDE, and cut off AH, EG, DF each equal to CB. Join CF, FG, GH, HC. Now the four △s ACH, CBF, FDG, GEH are evidently equal; therefore their sum is equal to four times the △ACH; but the △ACH is half the rectangle AC.AH (i. Cor. 2)—that is, equal to half the rectangle AC.CB. Therefore the sum of the four triangles is equal to 2AC.CB.
Again, the figure CFGH is a square [I. xlvi., Cor. 3], and equal to AC2 + AH2 [I. xlvii.]—that is, equal to AC2 + CB2. Hence the whole figure ABDE = AC2 + CB2 + 2AC.CB.
| Or thus: | AB | = AC + CB. | ||||||||
| Squaring, we get | AB2 = | AC2 + 2AC.CB + CB2. |
Cor. 1.—The parallelograms about the diagonal of a square are squares.
