BOOK III.
THEORY OF THE CIRCLE
________________
DEFINITIONS.
i. Equal circles are those whose radii are equal.
This is a theorem, and not a definition. For if two circles have equal radii, they are evidently congruent figures, and therefore equal. From this way of proving this theorem Props. xxvi.–xxix. follow as immediate inferences.
ii. A chord of a circle is the line joining two points in its circumference.
If the chord be produced both ways, the whole line is called a secant, and each of the parts into which a secant divides the circumference is called an arc—the greater the major conjugate arc, and the lesser the minor conjugate arc.—Newcomb.
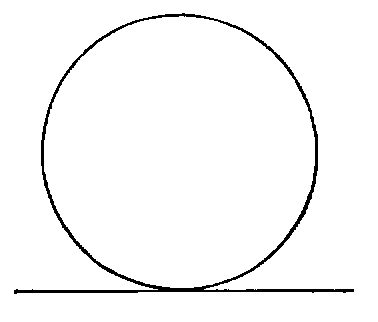
iii. A right line is said to touch a circle when it meets the circle, and, being produced both ways, does not cut it; the line is called a tangent to the circle, and the point where it touches it the point of contact.
In Modern Geometry a curve is considered as made up of an infinite number of points, which are placed in order along the curve, and then the secant through two consecutive points is a tangent. Euclid’s definition for a tangent is quite inadequate for any curve but the circle, and those derived from it by projection (the conic sections); and even for these the modern definition is better.
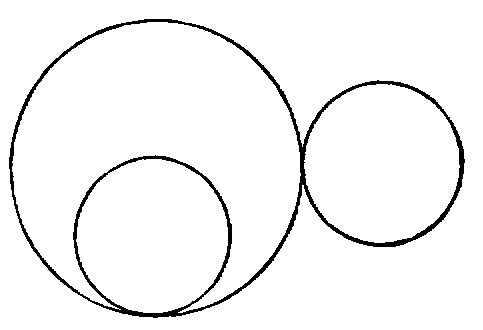
iv. Circles are said to touch one another when they meet, but do not intersect.
There are two species of contact:—
1. When each circle is external to the other.
2. When one is inside the other.
The following is the modern definition of curve-contact:— When two curves have two, three, four, &c., consecutive points common, they have contact of the first, second, third, &c., orders.
v. A segment of a circle is a figure bounded by a chord and one of the arcs into which it divides the circumference.
vi. Chords are said to be equally distant from the centre when the perpendiculars drawn to them from the centre are equal.
vii. The angle contained by two lines, drawn from any point in the circumference of a segment to the extremities of its chord, is called an angle in the segment.
viii. The angle of a segment is the angle contained between its chord and the tangent at either extremity.
A theorem is tacitly assumed in this Definition, namely, that the angles which the chord makes with the tangent at its extremities are equal. We shall prove this further on.
ix. An angle in a segment is said to stand on its conjugate arc.

x. Similar segments of circles are those that contain equal angles.
xi. A sector of a circle is formed of two radii and the arc included between them.
To a pair of radii may belong either of the two conjugate arcs into which their ends divide the circle.—Newcomb.
xii. Concentric circles are those that have the same centre.
xiii. Points which lie on the circumference of a circle are said to be concyclic.
xiv. A cyclic quadrilateral is one which is inscribed in a circle.
xv. It will be proper to give here an explanation of the extended meaning of the word angle in Modern Geometry. This extension is necessary in Trigonometry, in Mechanics—in fact, in every application of Geometry, and has been partly given in I. Def. ix.
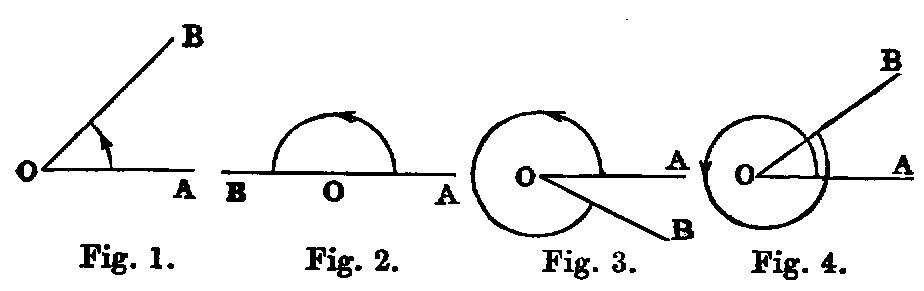
Thus, if a line OA revolve about the point O, as in figures 1, 2, 3, 4, until it comes into the position OB, the amount of the rotation from OA to OB is called an angle. From the diagrams we see that in fig. 1 it is less than two right angles; in fig. 2 it is equal to two right angles; in fig. 3 greater than two right angles, but less than four; and in fig. 4 it is greater than four right angles. The arrow-heads denote the direction or sense, as it is technically termed, in which the line OA turns. It is usual to call the direction indicated in the above figures positive, and the opposite negative. A line such as OA, which turns about a fixed point, is called a ray, and then we have the following definition:—
xvi. A ray which turns in the sense opposite to the hands of a watch describes a positive angle, and one which turns in the same direction as the hands, a negative angle.
PROP. I.—Problem.
To find the centre of a given circle (ADB).
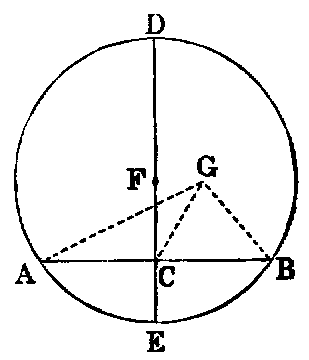
Sol.—Take any two points A, B in the circumference. Join AB. Bisect it in C. Erect CD at right angles to AB. Produce DC to meet the circle again in E. Bisect DE in F. Then F is the centre.
Dem.—If possible, let any other point G be the centre. Join GA, GC, GB. Then in the triangles ACG, BCG we have AC equal to CB (const.), CG common, and the base GA equal to GB, because they are drawn from G, which is, by hypothesis, the centre, to the circumference. Hence [I. viii.] the angle ACG is equal to the adjacent angle BCG, and therefore [I. Def. xiii.] each is a right angle; but the angle ACD is right (const.); therefore ACD is equal to ACG—a part equal to the whole—which is absurd. Hence no point can be the centre which is not in the line DE. Therefore F, the middle point of DE, must be the centre.
The foregoing proof may be abridged as follows:—
Because ED bisects AB at right angles, every point equally distant from, the points
A, B must lie in ED [I. x. Ex. 2]; but the centre is equally distant from A and B;
hence the centre must be in ED; and since it must be equally distant from E and D,
it must be the middle point of DE.
Cor. 1.—The line which bisects any chord of a circle perpendicularly passes through the centre of the circle.
Cor. 2.—The locus of the centres of the circles which pass through two fixed points is the line bisecting at right angles that connecting the two points.
Cor. 3.—If A, B, C be three points in the circumference of a circle, the lines bisecting perpendicularly the chords AB, BC intersect in the centre.
PROP. II.—Theorem.
If any two points (A, B) be taken in the circumference of a circle—1. The segment (AB) of the indefinite line through these points which lies between them falls within the circle. 2. The remaining parts of the line are without the circle.
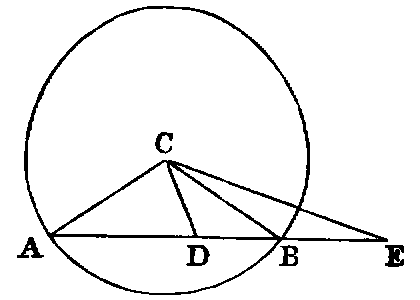
Dem.—1. Let C be the centre. Take any point D in AB. Join CA,CD,CB. Now the angle ADC is [I. xvi.] greater than ABC; but the angle ABC is equal to CAB [I. v.], because the triangle CAB is isosceles; therefore the angle ADC is greater than CAD. Hence AC is greater than CD [I. xix.]; therefore CD is less than the radius of the circle, consequently the point D must be within the circle (note on I. Def. xxiii.).
In the same manner every other point between A and B lies within the circle.
2. Take any point E in AB produced either way. Join CE. Then the angle ABC is greater than AEC [I. xvi.]; therefore CAB is greater than AEC. Hence CE is greater than CA, and the point E is without the circle.
We have added the second part of this Proposition. The indirect proof given of the first part in several editions of Euclid is very inelegant; it is one of those absurd things which give many students a dislike to Geometry.
Cor. 1.—Three collinear points cannot be concyclic.
Cor. 2.—A line cannot meet a circle in more than two points.
Cor. 3.—The circumference of a circle is everywhere concave towards the centre.
PROP. III.–Theorem.
If a line (AB) passing through the centre of a circle bisect a chord (CD), which does not pass through the centre, it cuts it at right angles. 2. If it cuts it at right angles, it bisects it.
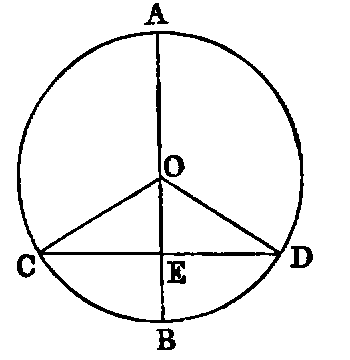
Dem.—1. Let O be the centre of the circle. Join OC, OD. Then the triangles CEO, DEO have CE equal to ED (hyp.), EO common, and OC equal to OD, because they are radii of the circle; hence [I. viii.] the angle CEO is equal to DEO, and they are adjacent angles. Therefore [I. Def. xiii.] each is a right angle. Hence AB cuts CD at right angles.
2. The same construction being made: because OC is equal to OD, the angle OCD is equal to ODC [I. v.], and CEO is equal to DEO (hyp.), because each is right. Therefore the triangles CEO, DEO have two angles in one respectively equal to two angles in the other, and the side EO common. Hence [I. xxvi.] the side CE is equal to ED. Therefore CD is bisected in E.
2. May be proved as follows:—
| OC2 = OE2+ | EC2 [I. xlvii.], and OD2 = OE2 + ED2; | |||||||||
| but | OC2 = | OD2; ∴ OE2 + EC2 = OE2 + ED2. | ||||||||
| Hence | EC2 = ED2, and EC = ED. |
Observation.—The three theorems, namely, Cor. 1., Prop. i., and Parts 1, 2, of Prop. iii., are so related, that any one being proved directly, the other two follow by the Rule of Identity.
Cor. 1.—The line which bisects perpendicularly one of two parallel chords of a circle bisects the other perpendicularly.
Cor. 2.—The locus of the middle points of a system of parallel chords of a circle is the diameter of the circle perpendicular to them all.
Cor. 3.—If a line intersect two concentric circles, its intercepts between the circles are equal.
Cor. 4.—The line joining the centres of two intersecting circles bisects their common chord perpendicularly.
Exercises.
1. If a chord of a circle subtend a right angle at a given point, the locus of its middle point is a circle.
2. Every circle passing through a given point, and having its centre on a given line, passes through another given point.
3. Draw a chord in a given circle which shall subtend a right angle at a given point, and be parallel to a given line.
PROP. IV.—Theorem.
Two chords of a circle (AB, CD) which are not both diameters cannot bisect
each other, though either may bisect the other.

Dem.—Let O be the centre. Let AB, CD intersect in E; then since AB, CD are not both diameters, join OE. If possible let AE be equal to EB, and CE equal to ED. Now, since OE passing through the centre bisects AB, which does not pass through the centre, it is at right angles to it; therefore the angle AEO is right. In like manner the angle CEO is right. Hence AEO is equal to CEO—that is, a part equal to the whole—which is absurd. Therefore AB and CD do not bisect each other.
Cor.—If two chords of a circle bisect each other, they are both diameters.
PROP. V.—Theorem.
If two circles (ABC, ABD) cut one another in any point (A), they are not
concentric.
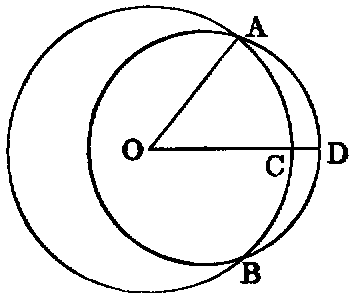
Dem.—If possible let them have a common centre at O. Join OA, and draw any other line OD, cutting the circles in C and D respectively. Then because O is the centre of the circle ABC, OA is equal to OC. Again, because O is the centre of the circle ABD, OA is equal to OD. Hence OC is equal to OD—a part equal to the whole—which is absurd. Therefore the circles are not concentric.
Exercises.
1. If two non-concentric circles intersect in one point, they must intersect in another point. For, let O, O′ be the centres, A the point of intersection; from A let fall the ⊥ AC on the line OO′. Produce AC to B, making BC = CA: then B is another point of intersection.
2. Two circles cannot have three points in common without wholly coinciding.
PROP. VI.—Theorem.
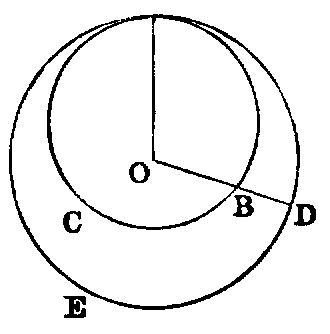
If one circle (ABC) touch another circle (ADE) internally in any point (A), it is not concentric with it.
Dem.—If possible let the circles be concentric, and let O be the centre of each. Join OA, and draw any other line OD, cutting the circles in the points B, D respectively. Then because O is the centre of each circle (hyp.), OB and OD are each equal to OA; therefore OB is equal to OD, which is impossible. Hence the circles cannot have the same centre.
PROP. VII.—Theorem.
If from any point (P) within a circle, which is not the centre, lines (PA, PB, PC, &c.), one of which passes through the centre, be drawn to the circumference, then—1. The greatest is the line (PA) which passes through the centre. 2. The production (PE) of this in the opposite direction is the least. 3. Of the others, that which is nearest to the line through the centre is greater than every one more remote. 4. Any two lines making equal angles with the diameter on opposite sides are equal. 5. More than two equal right lines cannot be drawn from the given point (P) to the circumference.
Dem.—1. Let O be the centre. Join OB. Now since O is the centre, OA is equal to OB: to each add OP, and we have AP equal to the sum of OB, OP; but the sum of OB, OP is greater than PB [I. xx.]. Therefore PA is greater than PB.
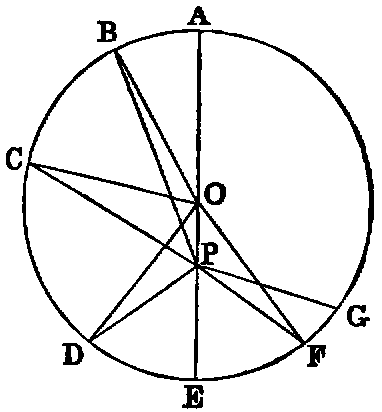
2. Join OD. Then [I. xx.] the sum of OP, PD is greater than OD; but OD is equal to OE [I. Def. xxx.]. Therefore the sum of OP, PD is greater than OE. Reject OP, which is common, and we have PD greater than PE.
3. Join OC; then two triangles POB, POC have the side OB equal to OC [I. Def. xxx.], and OP common; but the angle POB is greater than POC; therefore [I. xxiv.] the base PB is greater than PC. In like manner PC is greater than PD.
4. Make at the centre O the angle POF equal to POD. Join PF. Then the triangles POD, POF have the two sides OP, OD in one respectively equal to the sides OP, OF in the other, and the angle POD equal to the angle POF; hence PD is equal to PF [I. iv.], and the angle OPD equal to the angle OPF. Therefore PD and PF make equal angles with the diameter.
5. A third line cannot be drawn from P equal to either of the equal lines PD, PF. If possible let PG be equal to PD, then PG is equal to PF—that is, the line which is nearest to the one through the centre is equal to the one which is more remote, which is impossible. Hence three equal lines cannot be drawn from P to the circumference.
Cor. 1.—If two equal lines PD, PF be drawn from a point P to the circumference of a circle, the diameter through P bisects the angle DPF formed by these lines.
Cor. 2.—If P be the common centre of circles whose radii are PA, PB, PC, &c., then—1. The circle whose radius is the maximum line (PA) lies outside the circle ADE, and touches it in A [Def. iv.]. 2. The circle whose radius is the minimum line (PE) lies inside the circle ADE, and touches it in E. 3. A circle having any of the remaining lines (PD) as radius cuts ADE in two points (D, F).
Observation.—Proposition vii. affords a good illustration of the following important definition (see Sequel to Euclid, p. 13):—If a geometrical magnitude varies its position continuously according to any law, and if it retains the same value throughout, it is said to be a constant, such as the radius of a circle revolving round the centre; but if it goes on increasing for some time, and then begins to decrease, it is said to be a maximum at the end of the increase. Thus, in the foregoing figure, PA, supposed to revolve round P and meet the circle, is a maximum. Again, if it decreases for some time, and then begins to increase, it is a minimum at the commencement of the increase. Thus PE, supposed as before to revolve round P and meet the circle, is a minimum. Proposition viii. will give other illustrations.
PROP. VIII.—Theorem.
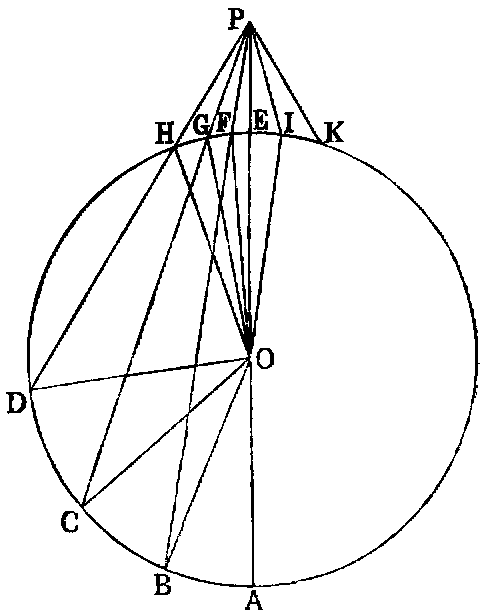
If from any point (P) outside a circle, lines (PA, PB, PC, &c.) be drawn to the concave circumference, then—1. The maximum is that which passes through the centre. 2. Of the others, that which is nearer to the one through the centre is greater than the one more remote. Again, if lines be drawn to the convex circumference—3. The minimum is that whose production passes through the centre. 4. Of the others, that which is nearer to the minimum is less than one more remote. 5. From the given point (P) there can be drawn two equal lines to the concave or the convex circumference, both of which make equal angles with the line passing through the centre. 6. More than two equal lines cannot be drawn from the given point (P) to either circumference.
Dem.—1. Let O be the centre. Join OB. Now since O is the centre, OA is equal to OB: to each add OP, and we have AP equal to the sum of OB, OP; but the sum of OB, OP is greater than BP [I. xx.]. Therefore AP is greater than BP.
2. Join OC, OD. The two triangles BOP, COP have the side OB equal to OC, and OP common, and the angle BOP greater than COP; therefore the base BP is greater than CP [I. xxiv.]. In like manner CP is greater than DP, &c.
3. Join OF. Now in the triangle OFP the sum of the sides OF, FP is greater than OP [I. xx.]; but OF is equal to OE [I. Def. xxx.]. Reject them, and FP will remain greater than EP.
4. Join OG, OH. The two triangles GOP, FOP have two sides GO, OP in one respectively equal to two sides FO, OP in the other; but the angle GOP is greater than FOP; therefore [I. xxiv.] the base GP is greater than FP. In like manner HP is greater than GP.
5. Make the angle POI equal POF [I. xxiii.]. Join IP. Now the triangles IOP, FOP have two sides IO, OP in one respectively equal to two sides FO, OP in the other, and the angle IOP equal to FOP (const.); therefore [I. iv.] IP is equal to FP.
6. A third line cannot be drawn from P equal to either of the lines IP, FP. For if possible let PK be equal to PF; then PK is equal to PI—that is, one which is nearer to the minimum equal to one more remote—which is impossible.
Cor. 1.—If PI be produced to meet the circle again in L, PL is equal to PB.
Cor. 2.—If two equal lines be drawn from P to either the convex or concave circumference, the diameter through P bisects the angle between them, and the parts of them intercepted by the circle are equal.
Cor. 3.—If P be the common centre of circles whose radii are lines drawn from P to the circumference of HDE, then—1. The circle whose radius is the minimum line (PE) has contact of the first kind with ADE [Def. iv.]. 2. The circle whose radius is the maximum line (PA) has contact of the second kind. 3. A circle having any of the remaining lines (PF) as radius intersects HDE in two points (F, I).