BOOK IV.
INSCRIPTION AND CIRCUMSCRIPTION OF TRIANGLES
AND OF REGULAR POLYGONS IN AND ABOUT CIRCLES
DEFINITIONS.
i. If two rectilineal figures be so related that the angular points of one lie on the sides of the other—1, the former is said to be inscribed in the latter; 2, the latter is said to be described about the former.
ii. A rectilineal figure is said to be inscribed in a circle when its angular points are on the circumference. Reciprocally, a rectilineal figure is said to be circumscribed to a circle when each side touches the circle.
iii. A circle is said to be inscribed in a rectilineal figure when it touches each side of the figure. Reciprocally, a circle is said to be circumscribed to a rectilineal figure when it passes through each angular point of the figure.
iv. A rectilineal figure which is both equilateral and equiangular is said to be regular.
Observation.—The following summary of the contents of the Fourth Book will assist the student in remembering it:—
1. It contains sixteen Propositions, of which four relate to triangles, four to squares, four to pentagons, and four miscellaneous Propositions.
2. Of the four Propositions occupied with triangles—
(α) One is to inscribe a triangle in a circle.
(β) Its reciprocal, to describe a triangle about a circle.
(γ) To inscribe a circle in a triangle.
(δ) Its reciprocal, to describe a circle about a triangle.
3. If we substitute in (α), (β), (γ), (δ) squares for triangles, and pentagons for triangles, we have the problems for squares and pentagons respectively.
4. Every Proposition in the fourth Book is a problem.
PROP. I.—Problem.
In a given circle (ABC) to place a chord equal to a given line (D) not greater
than the diameter.
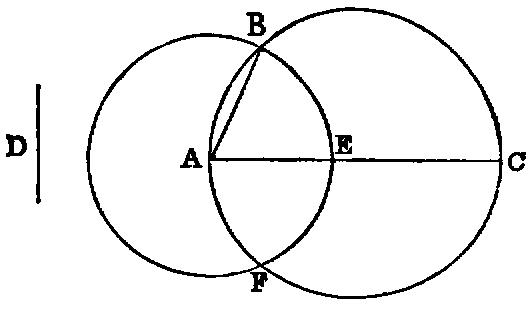
Sol.—Draw any diameter AC of the circle; then, if AC be equal to D, the thing required is done; if not, from AC cut off the part AE equal to D [I. iii.]; and with A as centre and AE as radius, describe the circle EBF, cutting the circle ABC in the points B, F. Join AB. Then AB is the chord required.
Dem.—Because A is the centre of the circle EBF, AB is equal to AE [I. Def. xxxii.]; but AE is equal to D (const.); therefore AB is equal to D.
PROP. II.—Problem.
In a given circle (ABC) to inscribe a triangle equiangular to a given triangle
(DEF).
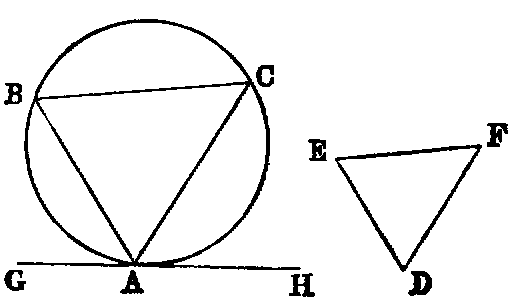
Sol.—Take any point A in the circumference, and at it draw the tangent GH; then make the angle HAC equal to E, and GAB equal to F [I. xxiii.] Join BC. ABC is a triangle fulfilling the required conditions.
Dem.—The angle E is equal to HAC (const.), and HAC is equal to the angle ABC in the alternate segment [III. xxxii.]. Hence the angle E is equal to ABC. In like manner the angle F is equal to ACB. Therefore [I. xxxii.] the remaining angle D is equal to BAC. Hence the triangle ABC inscribed in the given circle is equiangular to DEF.
PROP. III.—Problem.
About a given circle (ABC) to describe a triangle equiangular to a given
triangle (DEF).
Sol.—Produce any side DE of the given triangle both ways to G and H, and from the centre O of the circle draw any radius OA; make the angle AOB equal to GEF [I. xxiii.], and the angle AOC equal to HDF. At the points A, B, C draw the tangents LM, MN, NL to the given circle. LMN is a triangle fulfilling the required conditions.
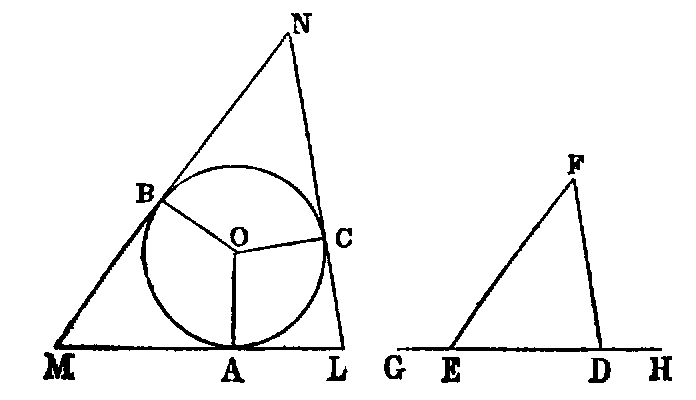
Dem.—Because AM touches the circle at A, the angle OAM is right. In like manner, the angle MBO is right; but the sum of the four angles of the quadrilateral OAMB is equal to four right angles. Therefore the sum of the two remaining angles AOB, AMB is two right angles; and [I. xiii.] the sum of the two angles GEF, FED is two right angles. Therefore the sum of AOB, AMB is equal to the sum of GEF, FED; but AOB is equal to GEF (const.). Hence AMB is equal to FED. In like manner, ALC is equal to EDF; therefore [I. xxxii.] the remaining angle BNC is equal to DFE. Hence the triangle LMN is equiangular to DEF.
PROP. IV.—Problem.
To inscribe a circle in a given triangle (ABC).
Sol.—Bisect any two angles A, B of the given triangle by the lines AO, BO; then O, their point of intersection, is the centre of the required circle.
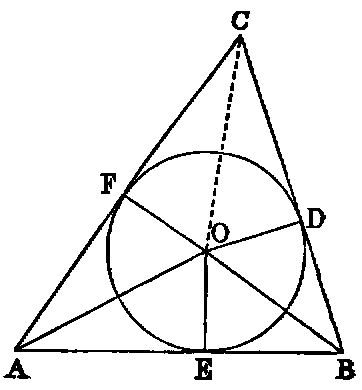
Dem.—From O let fall the perpendiculars OD, OE, OF on the sides of the triangle. Now, in the triangles OAE, OAF the angle OAE is equal to OAF (const.), and the angle AEO equal to AFO, because each is right, and the side OA common. Hence [I. xxvi.] the side OE is equal to OF. In like manner OD is equal to OF; therefore the three lines OD, OE, OF are all equal. And the circle described with O as centre and OD as radius will pass through the points E, F; and since the angles D, E, F are right, it will [III. xvi.] touch the three sides of the triangle ABC; and therefore the circle DEF is inscribed in the triangle ABC.
Exercises.

1. If the points O, C be joined, the angle C is bisected. Hence “the bisectors of the angles of a triangle are concurrent” (compare I. xxvi., Ex. 7).
2. If the sides BC, CA, AB of the triangle ABC be denoted by a, b, c, and half their sum by s, the distances of the vertices A, B, C of the triangle from the points of contact of the inscribed circle are respectively s − a, s − b, s − c.
3. If the external angles of the triangle ABC be bisected as in the annexed diagram, the three angular points O′, O′′, O′′′, of the triangle formed by the three bisectors will be the centres of three circles, each touching one side externally, and the other two produced. These three circles are called the escribed circles of the triangle ABC.
4. The distances of the vertices A, B, C from the points of contact of the escribed circle which touches AB externally are s − b, s − a, s.
5. The centre of the inscribed circle, the centre of each escribed circle, and two of the angular points of the triangle, are concyclic. Also any two of the escribed centres are concyclic with the corresponding two of the angular points of the triangle.
6. Of the four points O, O′, O′′, O′′′, any one is the orthocentre of the triangle formed by the remaining three.
7. The three triangles BCO′, CAO′′, ABO′′′ are equiangular.
8. The rectangle CO.CO′′′ = ab; AO.AO′ = bc; BO.BO′′ = ca.
9. Since the whole triangle ABC is made up of the three triangles AOB, BOC, COA, we see that the rectangle contained by the sum of the three sides, and the radius of the inscribed circle, is equal to twice the area of the triangle. Hence, if r denote the radius of the inscribed circle, rs = area of the triangle.
10. If r′ denote the radius of the escribed circle which touches the side a externally, it may be shown in like manner that r′(s − a) = area of the triangle.
11. rr′ = s − b.s − c.
12. Square of area = s.s − a.s − b.s − c.
13. Square of area = r.r′.r′′.r′′′.
14. If the triangle ABC be right-angled, having the angle C right,
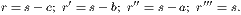
15. Given the base of a triangle, the vertical angle, and the radius of the inscribed, or any of the escribed circles: construct it.
PROP. V.—Problem.
To describe a circle about a given triangle (ABC).
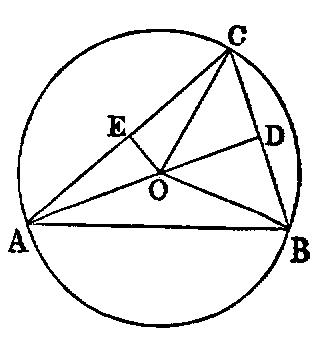
Sol.—Bisect any two sides BC, AC in the points D, E. Erect DO, EO at right angles to BC, CA; then O, the point of intersection of the perpendiculars, is the centre of the required circle.
Dem.—Join OA, OB, OC. The triangles BDO, CDO have the side BD equal CD (const.), and DO common, and the angle BDO equal to the angle CDO, because each is right. Hence [I. iv.] BO is equal to OC. In like manner AO is equal to OC. Therefore the three lines AO, BO, CO are equal, and the circle described with O as centre, and OA as radius, will pass through the points A, B, C, and be described about the triangle ABC.
Cor. 1.—Since the perpendicular from O on AB bisects it [III. iii.], we see that the perpendiculars at the middle points of the sides of a triangle are concurrent.
Def.—The circle ABC is called the circumcircle, its radius the circumradius, and its centre the circumcentre of the triangle.
Exercises.
1. The three perpendiculars of a triangle (ABC) are concurrent.
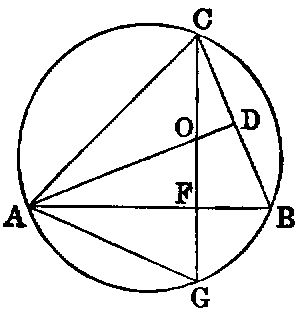
Dem.—Describe a circle about the triangle. Let fall the perpendicular CF. Produce CF to meet the circle in G. Make FO = FG. Join AG, AO. Produce AO to meet BC in D. Then the triangles GFA, OFA have the sides GF, FA in one equal to the sides OF, FA in the other, and the contained angles equal. Hence [I. iv.] the angle GAF equal OAF; but GAF = GCB [III. xxi.]; hence OAF = OCD, and FOA = DOC; hence OFA = ODC; but OFA is right, hence ODC is right. In like manner, if BO be joined to meet AC in E, BE will be perpendicular to AC. Hence the three perpendiculars pass through O, and are concurrent. This Proposition may be proved simply as follows:—
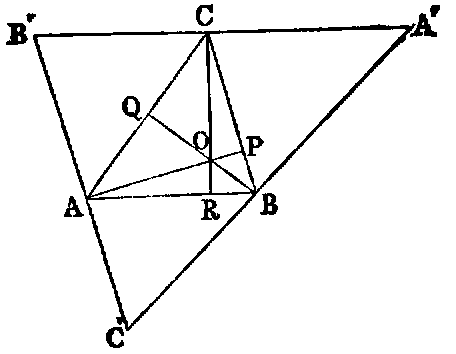
Draw parallels to the sides of the original triangle ABC through its vertices, forming a new triangle A′B′C′ described about ABC; then the three perpendiculars at the middle points of the sides of A′B′C′ are concurrent [v. Cor. 1], and these are evidently the perpendiculars from the vertices on the opposite sides of the triangle ABC (compare Ex. 16, Book I.).
Def.—The point O is called the orthocentre of the triangle ABC.
2. The three rectangles OA.OP, OB.OQ, OC.OR are equal.
Def.—The circle round O as centre, the square of whose radius is equal OA.OP = OB.OQ = OC.OR, is called the polar circle of the triangle ABC.
Observation.—If the orthocentre of the triangle ABC be within the triangle, the rectangles OA.OP, OB.OQ, OC.OR are negative, because the lines OA.OP, &c., are measured in opposite directions, and have contrary signs; hence the polar circle is imaginary; but it is real when the point O is without the triangle—that is, when the triangle has an obtuse angle.
3. If the perpendiculars of a triangle be produced to meet the circumscribed circle, the intercepts between the orthocentre and the circle are bisected by the sides of the triangle.
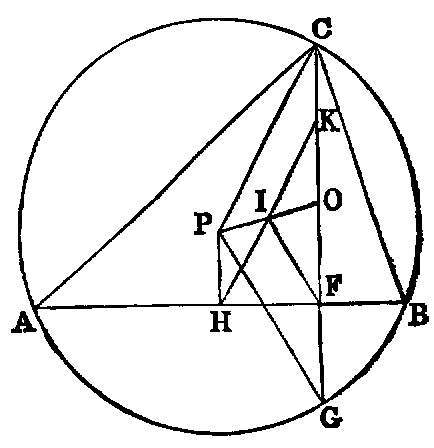
4. The point of bisection (I) of the line (OP) joining the orthocentre (O) to the circumference (P) of any triangle is equally distant from the feet of the perpendiculars, from the middle points of the sides, and from the middle points of the distances of the vertices from the orthocentre.
Dem.—Draw the perpendicular PH; then, since OF, PH are perpendiculars on AB, and OP is
bisected in I, it is easy to see that IH = IF. Again, since OP, OG are bisected in I,
F; IF = 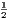 PG—that is, IF =
PG—that is, IF = 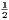 the radius. Hence the distance of I from the foot of
each perpendicular, and from the middle point of each side, is =
the radius. Hence the distance of I from the foot of
each perpendicular, and from the middle point of each side, is = 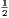 the radius. In like
manner, if OC be bisected in K, then IK =
the radius. In like
manner, if OC be bisected in K, then IK = 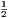 the radius. Hence we have the following
theorem:—The nine points made up of the feet of the perpendiculars, the middle points of
the sides, and the middle points of the lines from the vertices to the orthocentre, are
concyclic.
the radius. Hence we have the following
theorem:—The nine points made up of the feet of the perpendiculars, the middle points of
the sides, and the middle points of the lines from the vertices to the orthocentre, are
concyclic.
Def.—The circle through these nine points is called the “nine points circle” of the triangle.
5. The circumcircle of a triangle is the “nine points circle” of each of the four triangles formed by joining the centres of the inscribed and escribed circles.
6. The distances between the vertices of a triangle and its orthocentre are respectively the doubles of the perpendiculars from the circumcentre on the sides.
7. The radius of the “nine points circle” of a triangle is equal to half its circumradius.
PROP. VI.—Problem.
In a given circle (ABCD) to inscribe a square.

Sol.—Draw any two diameters AC, BD at right angles to each other. Join AB, BC, CD, DA. ABCD is a square.
Dem.—Let O be the centre. Then the four angles at O, being right angles, are equal. Hence the arcs on which they stand are equal [III. xxvi.], and hence the four chords are equal [III. xxix.]. Therefore the figure ABCD is equilateral.
Again, because AC is a diameter, the angle ABC is right [III. xxxi.]. In like manner the remaining angles are right. Hence ABCD is a square.
PROP. VII.—Problem.
About a given circle (ABCD) to describe a square.
Sol.—Through the centre O draw any two diameters at right angles to each other, and draw at the points A, B, C, D the lines HE, EF, FG, GH touching the circle. EFGH is a square.
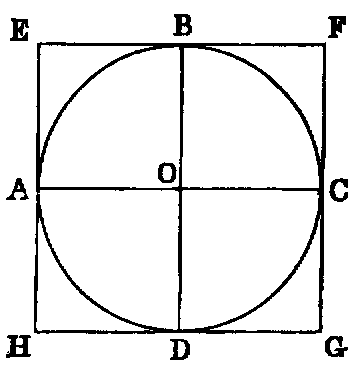
Dem.—Because AE touches the circle at A, the angle EAO is right [III. xviii.], and therefore equal to BOC, which is right (const.). Hence AE is parallel to OB. In like manner EB is parallel to AO; and since AO is equal to OB, the figure AOBE is a lozenge, and the angle AOB is right; hence AOBE is a square. In like manner each of the figures BC, CD, DA is a square. Hence the whole figure is a square.
Cor.—The circumscribed square is double of the inscribed square.