BOOK V.
THEORY OF PROPORTION
DEFINITIONS.
Introduction.—Every proposition in the theories of ratio and proportion is true for all descriptions of magnitude. Hence it follows that the proper treatment is the Algebraic. It is, at all events, the easiest and the most satisfactory. Euclid’s proofs of the propositions, in the Theory of Proportion, possess at present none but a historical interest, as no student reads them now. But although his demonstrations are abandoned, his propositions are quoted by every writer, and his nomenclature is universally adopted. For these reasons it appears to us that the best method is to state Euclid’s definitions, explain them, or prove them when necessary, for some are theorems under the guise of definitions, and then supply simple algebraic proofs of his propositions.
i. A less magnitude is said to be a part or submultiple of a greater magnitude, when the less measures the greater—that is, when the less is contained a certain number of times exactly in the greater.
ii. A greater magnitude is said to be a multiple of a less when the greater is measured by the less—that is, when the greater contains the less a certain number of times exactly.
iii. Ratio is the mutual relation of two magnitudes of the same kind with respect to quantity.
iv. Magnitudes are said to have a ratio to one another when the less can be multiplied so as to exceed the greater.
These definitions require explanation, especially Def. iii., which has the fault of conveying no precise meaning—being, in fact, unintelligible.
The following annotations will make them explicit:—
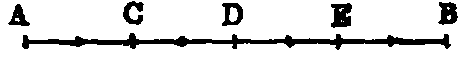
1. If an integer be divided into any number of equal parts, one, or the sum of any number of
these parts, is called a fraction. Thus, if the line AB represent the integer, and if it be
divided into four equal parts in the points C, D, E, then AC is 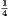 ; AD,
; AD, 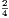 ; AE,
; AE, 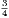 . Thus, a
fraction is denoted by two numbers parted by a horizontal line; the lower, called the
denominator, denotes the number of equal parts into which the integer is divided; and the upper,
called the numerator, denotes the number of these equal parts which are taken. Hence it
follows, that if the numerator be less than the denominator, the fraction is less than
unity. If the numerator be equal to the denominator, the fraction is equal to unity; and if
greater than the denominator, it is greater than unity. It is evident that a fraction is an
abstract quantity—that is, that its value is independent of the nature of the integer which is
divided.
. Thus, a
fraction is denoted by two numbers parted by a horizontal line; the lower, called the
denominator, denotes the number of equal parts into which the integer is divided; and the upper,
called the numerator, denotes the number of these equal parts which are taken. Hence it
follows, that if the numerator be less than the denominator, the fraction is less than
unity. If the numerator be equal to the denominator, the fraction is equal to unity; and if
greater than the denominator, it is greater than unity. It is evident that a fraction is an
abstract quantity—that is, that its value is independent of the nature of the integer which is
divided.
2. If we divide each of the equal parts AC, CD, DE, EB into two equal parts, the whole, AB,
will be divided into eight equal parts; and we see that AC = 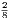 ; AD =
; AD = 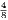 ; AE =
; AE = 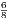 ; AB =
; AB = 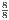 ; Now,
we saw in 1, that AE =
; Now,
we saw in 1, that AE = 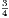 of the integer, and we have just shown that it is equal to
of the integer, and we have just shown that it is equal to 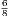 . Hence
. Hence 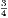 =
= 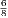 ;
but
;
but 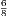 would be got from
would be got from 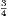 by multiplying its terms (numerator and denominator) by 2. Hence we
infer generally that multiplying the terms of any fraction by 2 does not alter its value. In like
manner it may be shown that multiplying the terms of a fraction by any whole number
does not alter its value. Hence it follows conversely, that dividing the terms of a fraction
by a whole number does not alter the value. Hence we have the following important
and fundamental theorem:—Two transformations can be made on any fraction without
changing its value; namely, its terms can be either multiplied or divided by any whole
number, and in either case the value of the new fraction is equal to the value of the original
one.
by multiplying its terms (numerator and denominator) by 2. Hence we
infer generally that multiplying the terms of any fraction by 2 does not alter its value. In like
manner it may be shown that multiplying the terms of a fraction by any whole number
does not alter its value. Hence it follows conversely, that dividing the terms of a fraction
by a whole number does not alter the value. Hence we have the following important
and fundamental theorem:—Two transformations can be made on any fraction without
changing its value; namely, its terms can be either multiplied or divided by any whole
number, and in either case the value of the new fraction is equal to the value of the original
one.
3. If we take any number, such as 3, and multiply it by any whole number, the product is called a multiple of 3. Thus 6, 9, 12, 15, &c., are multiples of 3; but 10, 13, 17, &c., are not, because the multiplication of 3 by any whole number will not produce them. Conversely, 3 is a submultiple, or measure, or part of 6, 9, 12, 15, &c., because it is contained in each of these without a remainder; but not of 10, 13, 17, &c., because in each case it leaves a remainder.
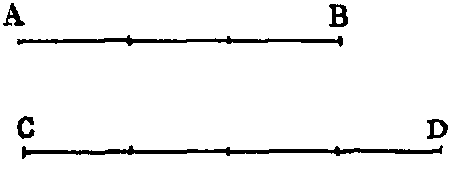
4. If we consider two magnitudes of the same kind, such as two lines AB, CD, and if we suppose
that AB is equal to 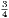 of CD, it is evident, if AB be divided into 3 equal parts, and CD into 4 equal
parts, that one of the parts into which AB is divided is equal to one of the parts into which CD is
divided. And as there are 3 parts in AB, and 4 in CD, we express this relation by saying that
AB has to CD the ratio of 3 to 4; and we denote it thus, 3 : 4. Hence the ratio 3 : 4
expresses the same idea as the fraction
of CD, it is evident, if AB be divided into 3 equal parts, and CD into 4 equal
parts, that one of the parts into which AB is divided is equal to one of the parts into which CD is
divided. And as there are 3 parts in AB, and 4 in CD, we express this relation by saying that
AB has to CD the ratio of 3 to 4; and we denote it thus, 3 : 4. Hence the ratio 3 : 4
expresses the same idea as the fraction 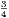 . In fact, both are different ways of expressing and
writing the same thing. When written 3 : 4 it is called a ratio, and when
. In fact, both are different ways of expressing and
writing the same thing. When written 3 : 4 it is called a ratio, and when 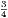 a fraction.
In the same manner it can be shown that every ratio whose terms are commensurable
can be converted into a fraction; and, conversely, every fraction can be turned into a
ratio.
a fraction.
In the same manner it can be shown that every ratio whose terms are commensurable
can be converted into a fraction; and, conversely, every fraction can be turned into a
ratio.
From this explanation we see that the ratio of any two commensurable magnitudes is the same as the ratio of the numerical quantities which denote these magnitudes. Thus, the ratio of two commensurable lines is the ratio of the numbers which express their lengths, measured with the same unit. And this may be extended to the case where the lines are incommensurable. Thus, if a be the side and b the diagonal of a square, the ratio of a : b is
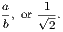
When two quantities are incommensurable, such as the diagonal and the side of a square, although their ratio is not equal to that of any two commensurable numbers, yet a series of pairs of fractions can be found whose difference is continually diminishing, and which ultimately becomes indefinitely small; such that the ratio of the incommensurable quantities is greater than one, and less than the other fraction of each pair. These fractions are called convergents. By their means we can approximate as nearly as we please to the exact value of the ratio. In the case of the diagonal and the side of a square, the following are the pairs of convergents:—
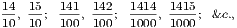
and the ratio is intermediate to each pair. It is evident we may continue the series as far as we
please. Now if we denote the first of any of the foregoing pairs of fractions by 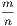 , the second will be
, the second will be
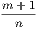 ; and in general, in the case of two incommensurable quantities, two fractions
; and in general, in the case of two incommensurable quantities, two fractions 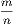 and
and 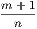 can always be found, where n can be made as large as we please, one of which is less and the
other greater than the true value of the ratio. For let a and b be the incommensurable
quantities; then, evidently, we cannot find two multiples na, mb, such that na = mb. In this
case, take any multiple of a, such as na, then this quantity must lie between some two
consecutive multiples of b, such as mb, and (m + 1)b; therefore
can always be found, where n can be made as large as we please, one of which is less and the
other greater than the true value of the ratio. For let a and b be the incommensurable
quantities; then, evidently, we cannot find two multiples na, mb, such that na = mb. In this
case, take any multiple of a, such as na, then this quantity must lie between some two
consecutive multiples of b, such as mb, and (m + 1)b; therefore 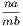 is greater than unity, and
is greater than unity, and
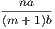 less than unity. Hence
less than unity. Hence 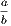 lies between
lies between 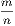 and
and 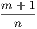 . Now, since the difference
between
. Now, since the difference
between 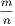 and
and 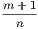 namely,
namely, 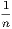 becomes small as n increases, we see that the difference
between the ratio of two incommensurable quantities and that of two commensurable
numbers m and n can be made as small as we please. Hence, ultimately, the ratio of
incommensurable quantities may be regarded as the limit of the ratio of commensurable
quantities.
becomes small as n increases, we see that the difference
between the ratio of two incommensurable quantities and that of two commensurable
numbers m and n can be made as small as we please. Hence, ultimately, the ratio of
incommensurable quantities may be regarded as the limit of the ratio of commensurable
quantities.
5. The two terms of a ratio are called the antecedent and the consequent. These correspond to the numerator and the denominator of a fraction. Hence we have the following definition:—“A ratio is the fraction got by making the antecedent the numerator and the consequent the denominator.”
6. The reciprocal of a ratio is the ratio obtained by interchanging the antecedent and the consequent. Thus, 4 : 3 is the reciprocal of the ratio 3 : 4. Hence we have the following theorem:—“The product of a ratio and its reciprocal is unity.”
7. If we multiply any two numbers, as 5 and 7, by any number such as 4, the products 20, 28 are called equimultiples of 5 and 7. In like manner, 10 and 15 are equimultiples of 2 and 3, and 18 and 30 of 3 and 5, &c.
v. The first of four magnitudes has to the second the same ratio which the third has to the fourth, when any equimultiples whatsoever of the first and third being taken, and any equimultiples whatsoever of the second and fourth, if, according as the multiple of the first is greater than, equal to, or less than the multiple of the second, the multiple of the third is greater than, equal to, or less than the multiple of the fourth.
vi. Magnitudes which have the same ratio are called proportionals. When four magnitudes are proportionals, it is usually expressed by saying, “The first is to the second as the third is to the fourth.”
viii. Analogy or proportion is the similitude of ratios.
We have given the foregoing definitions in the order of Euclid, as given by Simson, Lardner, and others;2 2Except that viii. is put before vii., because it relates, as v. and vi., to the equality of ratios, whereas vii. is a test of their inequality. but it is evidently an inverted order; for vi. viii. are definitions of proportion, and v. is only a test of proportion, and is not a definition but a theorem, and one which, instead of being taken for granted, requires proof. The following explanations will give the student clear conceptions of their meaning:—
1. If we take two ratios, such as 6 : 9 and 10 : 15, which are each equal to the same thing (in this
example each is equal to 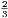 ), they are equal to one another (I. Axiom i.). Then we may write it
thus—
), they are equal to one another (I. Axiom i.). Then we may write it
thus—
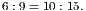
This would be the most intelligible way, but it is not the usual one, which is as follows:—6 : 9 :: 10 : 15. In this form it is called a proportion. Hence a proportion consists of two ratios which are asserted by it to be equal. Its four terms consist of two antecedents and two consequents. The 1st and 3rd terms are the antecedents, and the 2nd and 4th the consequents. Also the first and last terms are called the extremes, and the two middle terms the means.
2. Since a proportion consists of two equal ratios, and each ratio can be written as a fraction, whenever we have a proportion such as
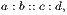
we can write it in the form of two equal fractions. Thus:
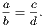
Conversely, an equation between two fractions can be put into a proportion. By means of these simple principles all the various properties of proportion can be proved in the most direct and easy manner.
3. If we take the proportion a : b :: c : d, and multiply the first and third terms, each by m, and second and fourth, each by n, we get the four multiples, ma, nb, mc, nd; and we want to prove that if ma is greater than nb, mc is greater than nd; if equal, equal; and if less, less.
| Dem.—Since | a : b | :: c : d, | |||||||||
| we have | 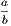 | = 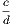 . . | |||||||||
Hence, multiplying each by 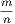 we get we get | |||||||||||
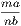 | = 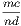 . . | ||||||||||
Now, it is evident that if 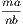 is greater than unity,
is greater than unity, 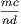 is greater than unity; but if
is greater than unity; but if
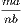 is greater than unity, ma is greater than nb; and if
is greater than unity, ma is greater than nb; and if 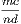 is greater than unity, mc is
greater than nd. In like manner, if ma be equal to nb, mc is equal to nd; and if less,
less.
is greater than unity, mc is
greater than nd. In like manner, if ma be equal to nb, mc is equal to nd; and if less,
less.
The foregoing is an easy proof of the converse of the theorem which is contained in Euclid’s celebrated Fifth Definition.
Next, to prove Euclid’s theorem—that if, according as the multiple of the first of four magnitudes is greater than, equal to, or less than the multiple of the second, the multiple of the third is greater than, equal to, or less than the multiple of the fourth; the ratio of the first to the second is equal to the ratio of the third to the fourth.
Dem.—Let, a, b, c, d be the four magnitudes. First suppose that a and b are commensurable, then it is evident that we can take multiples na, mb, such that na = mb. Hence, by hypothesis, nc = md. Thus,
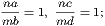
| therefore | 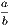 = = 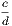 . . |
Next, suppose a and b are incommensurable. Then, as in a recent note, we can find two numbers m
and n, such that 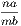 is greater than unity, but
is greater than unity, but 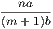 less than unity. Hence
less than unity. Hence 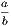 lies between
lies between 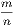 and
and  . Now, since by hypothesis, when
. Now, since by hypothesis, when 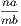 is greater than unity,
is greater than unity, 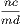 is greater than unity; and
when
is greater than unity; and
when 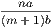 is less than unity,
is less than unity, 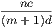 is less than unity. Hence, since
is less than unity. Hence, since 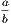 lies between
lies between 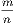 and
and 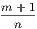 ,
, 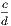 lies between the same quantities. Therefore the difference between
lies between the same quantities. Therefore the difference between 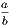 and
and
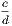 is less than
is less than 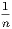 ; and since n may be as large as we please, the difference is nothing;
therefore
; and since n may be as large as we please, the difference is nothing;
therefore

vii. When of the multiples of four magnitudes (taken as in Def. v.) the multiple of the first is greater than that of the second, but the multiple of the third not greater than that of the fourth, the first has to the second a greater ratio than the third has to the fourth.
This, instead of being a definition, is a theorem. We have altered the last clause from that given in Simson’s Euclid, which runs thus:—“The first is said to have to the second a greater ratio than the third has to the fourth.” This is misleading, as it implies that it is, by convention, that the first ratio is greater than the second, whereas, in fact, such is not the case; for it follows from the hypothesis that the first ratio is greater than the second; and if it did not, it could not be made so by definition. We have made a similar change in the enunciation of the Fifth Definition.
Let a, b, c, d be the four magnitudes, and m and n the multiples taken, it is required to prove, that if ma be greater than nb, but mc not greater than nd, that the ratio a : b is greater than the ratio c : d.
Dem.—Since ma is greater than nb, but mc not greater than nd, it is evident that
 | is greater than  ; ; | ||||||||||
| therefore |  | is greater than 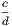 ; ; |
that is, the ratio a : b is greater than the ratio c : d.
ix. Proportion consists of three terms at least.
This has the same fault as some of the others—it is not a definition, but an inference. It occurs
when the means in a proportion are equal, so that, in fact, there are four terms. As an illustration,
let us take the numbers 4, 6, 9. Here the ratio of 4 : 6 is  , and the ratio of 6 : 9 is
, and the ratio of 6 : 9 is 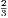 , so that 4, 6, 9
are continued proportionals; but, in reality, there are four terms, for the full proportion is
4 : 6 :: 6 : 9.
, so that 4, 6, 9
are continued proportionals; but, in reality, there are four terms, for the full proportion is
4 : 6 :: 6 : 9.
x. When three magnitudes are continual proportionals, the first is said to have to the third the duplicate ratio of that which it has to the second.
xi. When four magnitudes are continual proportionals, the first is said to have to the fourth the triplicate ratio of that which it has to the second.
xii. When there is any number of magnitudes of the same kind greater than two, the first is said to have to the last the ratio compounded of the ratios of the first to the second, of the second to the third, of the third to the fourth, &c.
We have placed these definitions in a group; but their order is inverted, and, as we shall see, Def. xii. is a theorem, and x. and xi. are only inferences from it.
1. If we have two ratios, such as 5 : 7 and 3 : 4, and if we convert each ratio into a fraction, and
multiply these fractions together, we get a result which is called the ratio compounded of the two
ratios; viz. in this example it is 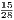 , or 15 : 28. It is evident we get the same result if we multiply
the two antecedents together for a new antecedent, and the two consequents for a new
consequent. Hence we have the following definition:—“The ratio compounded of any
number of ratios it the ratio of the product of all the antecedents to the product of all the
consequents.”
, or 15 : 28. It is evident we get the same result if we multiply
the two antecedents together for a new antecedent, and the two consequents for a new
consequent. Hence we have the following definition:—“The ratio compounded of any
number of ratios it the ratio of the product of all the antecedents to the product of all the
consequents.”
2. To prove the theorem contained in Def. xii.
Let the magnitudes be a, b, c, d. Then the ratio of
| 1st : 2nd | = 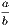 , , | ||
| 2nd : 3rd | = 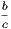 , , | ||
| 3rd : 4th | = 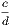 . . |
Hence the ratio compounded of the ratio of 1st : 2nd, of 2nd : 3rd, of 3rd : 4th

3. If three magnitudes be proportional, the ratio of the 1st : 3rd is equal to the square of the ratio of the 1st : 2nd. For the ratio of the 1st : 3rd is compounded of the ratio of the 1st : 2nd, and of the ratio of the 2nd : 3rd; and since these ratios are equal, the ratio compounded of them will be equal to the square of one of them.
Or thus: Let the proportionals be a, b, c, that is, let a : b :: b : c; hence we have

And multiplying each by  , we get
, we get
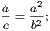
or a : c :: a2 : b2—that is, 1st : 3rd :: square of 1st : square of 2nd. Now, the ratio of 1st : 3rd is, by Def. x., the duplicate ratio of 1st : 2nd. Hence the duplicate ratio of two magnitudes means the square of their ratio, or, what is the same thing, the ratio of their squares (see Book VI. xx.).
4. If four magnitudes be continual proportionals, the ratio of 1st : 4th is equal to the cube of the ratio of 1st : 2nd. This may be proved exactly like 3. Hence we see that what Euclid calls triplicate ratio of two magnitudes is the ratio of their cubes, or the cube of their ratio.
We also see that there is no necessity to introduce extraneous magnitudes for the purpose of defining duplicate and triplicate ratios, as Euclid does. In fact, the definitions by squares and cubes are more explicit.
xiii. In proportionals, the antecedent terms are called homologous to one another; as also the consequents to one another.
If one proportion be given, from it an indefinite number of other proportions can be inferred, and a great part of the theory of proportion consists in proving the truth of these derived proportions. Geometers make use of certain technical terms to denote the most important of these processes. We shall indicate these terms by including them in parentheses in connexion with the Propositions to which they refer. They are useful as indicating, by one word, the whole enunciation of a theorem.