BOOK VI.
APPLICATION OF THE THEORY OF PROPORTION
DEFINITIONS.
i. Similar Rectilineal Figures are those whose several angles are equal, each to each, and whose sides about the equal angles are proportional.
Similar figures agree in shape; if they agree also in size, they are congruent.
1. When the shape of a figure is given, it is said to be given in species. Thus a triangle whose angles are given is given in species. Hence similar figures are of the same species.
2. When the size of a figure is given, it is said to be given in magnitude; for instance, a square whose side is of given length.
3. When the place which a figure occupies is known, it is said to be given in position.
ii. A right line is said to be cut at a point in extreme and mean ratio when the whole line is to the greater segment as the greater segment is to the less.
iii. If three quantities of the same kind be in continued proportion, the middle term is called a mean proportional between the other two.
Magnitudes in continued proportion are also said to be in geometrical progression.
iv. If four quantities of the same kind be in continued proportion, the two middle terms are called two mean proportionals between the other two.
v. The altitude of any figure is the length of the perpendicular from its highest point to its base.
vi. Two corresponding angles of two figures have the sides about them reciprocally proportional, when a side of the first is to a side of the second as the remaining side of the second is to the remaining side of the first.
This is evidently equivalent to saying that a side of the first is to a side of the second in the reciprocal ratio of the remaining side of the first to the remaining side of the second.
PROP. I.—Theorem.
Triangles (ABC, ACD) and parallelograms (EC, CF) which have the same
altitude are to one another as their bases (BC, CD).
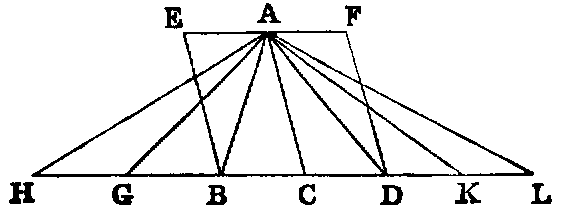
Dem.—Produce BD both ways, and cut off any number of parts BG, GH, &c., each equal to CB, and any number DK, KL, each equal to CD. Join AG, AH, AK, AL.
Now, since the several bases CB, BG, GH are all equal, the triangles ACB, ABG, AGH are also all equal [I. xxxviii.]. Therefore the triangle ACH is the same multiple of ACB that the base CH is of the base CB. In like manner, the triangle ACL is the same multiple of ACD that the base CL is of the base CD; and it is evident that [I. xxxviii.] if the base HC be greater than CL, the triangle HAC is greater than CAL; if equal, equal; and if less, less. Now we have four magnitudes: the base BC is the first, the base CD the second, the triangle ABC the third, and the triangle ACD the fourth. We have taken equimultiples of the first and third, namely, the base CH, and the triangle ACH; also equimultiples of the second and fourth, namely, the base CL, and the triangle ACL; and we have proved that according as the multiple of the first is greater than, equal to, or less than the multiple of the second, the multiple of the third is greater than, equal to, or less than the multiple of the fourth. Hence [V. Def. v.] the base BC : CD :: the triangle ABC : ACD.
2. The parallelogram EC is double of the triangle ABC [I. xxxiv.], and the parallelogram CF is double of the triangle ACD. Hence [V. xv.] EC : CF :: the triangle ABC : ACD; but ABC : ACD :: BC : CD (Part I.). Therefore [V. xi.] EC : CF :: the base BC : CD.
Or thus: Let A, A′ denote the areas of the triangles ABC, ACD, respectively, and P their common altitude; then [II. i., Cor. 1],
A =  P.BC, A′ = P.BC, A′ = 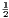 P.CD. P.CD. | |||||||||||
| Hence | 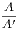 = = 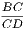 , or A : A′ :: BC : CD. , or A : A′ :: BC : CD. |
In extending this proof to parallelograms we have only to use P instead of 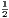 P.
P.
PROP. II.—Theorem.
If a line (DE) be parallel to a side (BC) of a triangle (ABC), it divides the remaining sides, measured from the opposite angle (A), proportionally; and, conversely, If two sides of a triangle, measured from an angle, be cut proportionally, the line joining the points of section is parallel to the third side.
1. It is required to prove that AD : DB :: AE : EC.
Dem.—Join BE, CD. The triangles BDE, CED are on the same base DE, and between the same parallels BC, DE. Hence [I. xxxvii.] they are equal, and therefore [V. vii.] the triangle ADE : BDE :: ADE : CDE;
| but | ADE | : BDE :: AD : DB [i.], | |||||||||
| and | ADE | : CDE :: AE : EC [i.]. | |||||||||
| Hence | AD | : DB :: AE : EC. |
2. If AD : DB :: AE : EC, it is required to prove that DE is parallel to BC.
Dem.—Let the same construction be made;
| then | AD : DB :: the triangle ADE : BDE [i.]. | ||||||||||
| and | AE : EC :: the triangle ADE : CDE [i.]; | ||||||||||
| but | AD : DB :: AE : EC (hyp.). | ||||||||||
| Hence | ADE : BDE :: ADE : CDE. |
Therefore [V. ix.] the triangle BDE is equal to CDE, and they are on the same base DE, and on the same side of it; hence they are between the same parallels [I. xxxix.]. Therefore DE is parallel to BC.
Observation.—The line DE may cut the sides AB, AC produced through B, C, or through the angle A; but evidently a separate figure for each of these cases is unnecessary.
Exercise.
If two lines be cut by three or more parallels, the intercepts on one are proportional to the corresponding intercepts on the other.
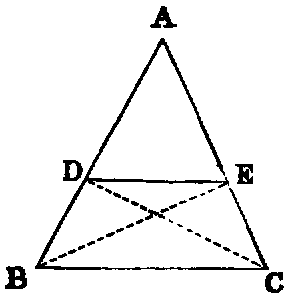
PROP. III.—Theorem.
If a line (AD) bisect any angle (A) of a triangle (ABC), it divides the opposite side (BC) into segments proportional to the adjacent sides. Conversely, If the segments (BD, DC) into which a line (AD) drawn from any angle (A) of a triangle divides the opposite side be proportional to the adjacent sides, that line bisects the angle (A).
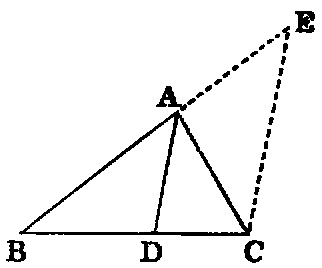
Dem.—1. Through C draw CE parallel to AD, to meet BA produced in E. Because BA meets the parallels AD, EC, the angle BAD [I. xxix.] is equal to AEC; and because AC meets the parallels AD, EC, the angle DAC is equal to ACE; but the angle BAD is equal to DAC (hyp.); therefore the angle ACE is equal to AEC; therefore AE is equal to AC [I. vi.]. Again, because AD is parallel to EC, one of the sides of the triangle BEC, BD : DC :: BA : AE [ii.]; but AE has been proved equal to AC. Therefore BD : DC :: BA : AC.
2. If BD : DC :: BA : AC, the angle BAC is bisected.
Dem.—Let the same construction be made.
Because AD is parallel to EC, BA : AE :: BD : DC [ii.]; but BD : DC :: BA : AC (hyp.). Therefore [V. xi.] BA : AE :: BA : AC, and hence [V. ix.] AE is equal to AC; therefore the angle AEC is equal to ACE; but AEC is equal to BAD [I. xxix.], and ACE to DAC; hence BAD is equal to DAC, and the line AD bisects the angle BAC.
Exercises.
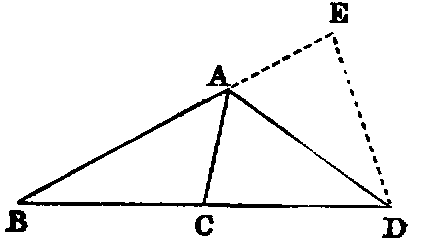
1. If the line AD bisect the external vertical angle CAE, BA : AC :: BD : DC, and conversely.
Dem.—Cut off AE = AC. Join ED. Then the triangles ACD, AED are evidently congruent; therefore the angle EDB is bisected; hence [iii.] BA : AE :: BD : DE; or BA : AC :: BD : DC.
2. Exercise 1 has been proved by quoting Proposition iii. Prove it independently, and prove iii. as an inference from it.
3. The internal and the external bisectors of the vertical angle of a triangle divide the base harmonically (see Definition, p. 191).
4. Any line intersecting the legs of any angle is cut harmonically by the internal and external bisectors of the angle.
5. Any line intersecting the legs of a right angle is cut harmonically by any two lines through its vertex which make equal angles with either of its sides.
6. If the base of a triangle be given in magnitude and position, and the ratio of the sides, the locus of the vertex is a circle which divides the base harmonically in the ratio of the sides.
7. If a, b, c denote the sides of a triangle ABC, and D, D′ the points where the internal and external bisectors of A meet BC; prove
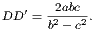
8. In the same case, if E, E′, F, F′ be points similarly determined on the sides CA, AB, respectively; prove
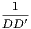 + + 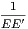 + + 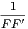 = 0, = 0, | |||
| and | 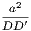 + +  + +  = 0. = 0. |
PROP. IV.—Theorem.
The sides about the equal angles of equiangular triangles (BAC, CDE) are proportional, and those which are opposite to the equal angles are homologous.
Dem.—Let the sides BC, CE, which are opposite to the equal angles A and D, be conceived to be placed so as to form one continuous line, the triangles being on the same side, and so that the equal angles BCA, CED may not have a common vertex.
Now, the sum of the angles ABC, BCA is less than two right angles; but BCA is equal to BED (hyp.). Therefore the sum of the angles ABE, BED is less than two right angles; hence [I., Axiom xii.] the lines AB, ED will meet if produced. Let them meet in F. Again, because the angle BCA is equal to BEF, the line CA [I. xxviii.] is parallel to EF. In like manner, BF is parallel to CD; therefore the figure ACDF is a parallelogram; hence AC is equal to DF, and CD is equal to AF. Now, because AC is parallel to FE, BA : AF :: BC : CE [ii.]; but AF is equal to CD, therefore BA : CD :: BC : CE; hence [V. xvi.]; AB : BC :: DC : CE. Again, because CD is parallel to BF, BC : CE :: FD : DE; but FD is equal to AC, therefore BC : CE :: AC : DE; hence [V. xvi.] BC : AC :: CE : DE. Therefore we have proved that AB : BC :: DC : CE, and that BC : CA :: CE : ED. Hence (ex aequali) AB : AC :: DC : DE. Therefore the sides about the equal angles are proportional.
This Proposition may also be proved very simply by superposition. Thus (see fig., Prop. ii.): let the two triangles be ABC, ADE; let the second triangle ADE be conceived to be placed on ABC, so that its two sides AD, AE may fall on the sides AB, AC; then, since the angle ADE is equal to ABC, the side DE is parallel to BC. Hence [ii.] AD : DB :: AE : EC; hence AD : AB :: AE : AC, and [V. xvi.] AD : AE :: AB : AC. Therefore the sides about the equal angles BAC, DAE are proportional, and similarly for the others.
It can be proved by this Proposition that two lines which meet at infinity are parallel. For, let I denote the point at infinity through which the two given lines pass, and draw any two parallels intersecting them in the points A, B; A′, B′; then the triangles AIB, A′IB′ are equiangular; therefore AI : AB :: A′I : A′B′; but the first term of the proportion is equal to the third; therefore [V. xiv.] the second term AB is equal to the fourth A′B′, and, being parallel to it, the lines AA′, BB′ [I. xxxiii.] are parallel.
Exercises.
1. If two circles intercept equal chords AB, A′B′ on any secant, the tangents AT, A′T to the circles at the points of intersection are to one another as the radii of the circles.
2. If two circles intercept on any secant chords that have a given ratio, the tangents to the circles at the points of intersection have a given ratio, namely, the ratio compounded of the direct ratio of the radii and the inverse ratio of the chords.
3. Being given a circle and a line, prove that a point may be found, such that the rectangle of the perpendiculars let fall on the line from the points of intersection of the circle with any chord through the point shall be given.
4. AB is the diameter of a semicircle ADB; CD a perpendicular to AB; draw through A a chord AF of the semicircle meeting CD in E, so that the ratio CE : EF may be given.
PROP. V.–Theorem.
If two triangles (ABC, DEF) have their sides proportional (BA : AC :: ED : DF; AC : CB :: DF : FE) they are equiangular, and those angles are equal which are subtended by the homologous sides.
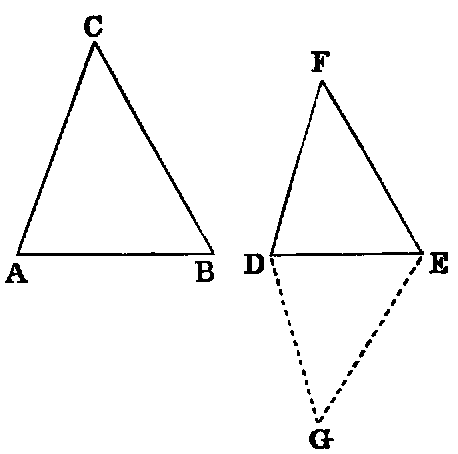
Dem.—At the points D, E make the angles EDG, DEG equal to the angles A, B of the triangle ABC. Then [I. xxxii.] the triangles ABC, DEG are equiangular.
| Therefore | BA : AC | :: ED : DG [iv.]; | |||||
| but | BA : AC | :: ED : DF (hyp.). |
Therefore DG is equal to DF. In like manner it may be proved that EG is equal to EF. Hence the triangles EDF, EDG have the sides ED, DF in one equal to the sides ED, DG in the other, and the base EF equal to the base EG. Hence [I. viii.] they are equiangular; but the triangle DEG is equiangular to ABC. Therefore the triangle DEF is equiangular to ABC.
Observation.—In VI. Def. i. two conditions are laid down as necessary for the similitude of rectilineal figures. 1. The equality of angles; 2. The proportionality of sides. Now, from Propositions iv. and v., we see that if two triangles possess either condition, they also possess the other. Triangles are unique in this respect. In all other rectilineal figures one of the conditions may exist without the other. Thus, two quadrilaterals may have their sides proportional without having equal angles, or vice versâ.