BOOK XI.
THEORY OF PLANES, COPLANAR LINES, AND SOLID ANGLES

i. When two or more lines are in one plane they are said to be coplanar.

ii. The angle which one plane makes with another is called a dihedral angle.

iii. A solid angle is that which is made by more than two plane angles, in different planes, meeting in a point.

iv. The point is called the vertex of the solid angle.

v. If a solid angle be composed of three plane angles it is called a trihedral angle; if of four, a tetrahedral angle; and if of more than four, a polyhedral angle.

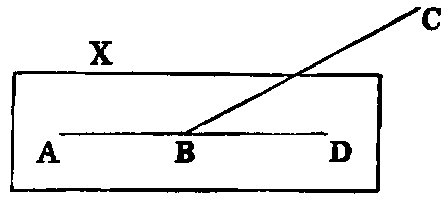
Dem.—Since AB is in the plane X, it can be produced in it [Bk. I. Post. ii.]; let it be produced to D. Then, if BC be not in X, let any other plane passing through AD be turned round AD until it passes through the point C. Now, because the points B, C are in this second plane, the line BC [I., Def. vi.] is in it. Therefore the two right lines ABC, ABD lying in one plane have a common segment AB, which is impossible. Therefore, &c.

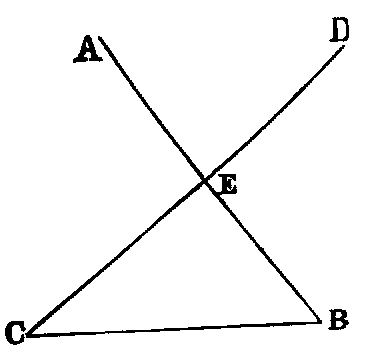
Two right lines (AB, CD) which intersect one another in any point (E) are coplanar, and so also are any three right lines (EC, CB, BE) which form a triangle.

Dem.—Let any plane pass through EB, and be turned round it until it passes through C. Then because the points E, C are in this plane, the right line EC is in it [I., Def. vi.]. For the same reason the line BC is in it. Therefore the lines EC, CB, BE are coplanar; but AB and CD are two of these lines. Hence AB and CD are coplanar.

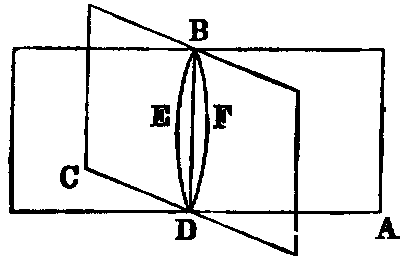
Dem.—If not from B to D, draw in the plane AB the right line BED, and in the plane BC the right line BFD. Then the right lines BED, BFD enclose a space, which [I., Axiom x.] is impossible. Therefore the common section BD of the two planes must be a right line.

If a right line (EF) be perpendicular to each of two intersecting lines (AB, CD), it will be perpendicular to any line GH, which is both coplanar and concurrent with them.

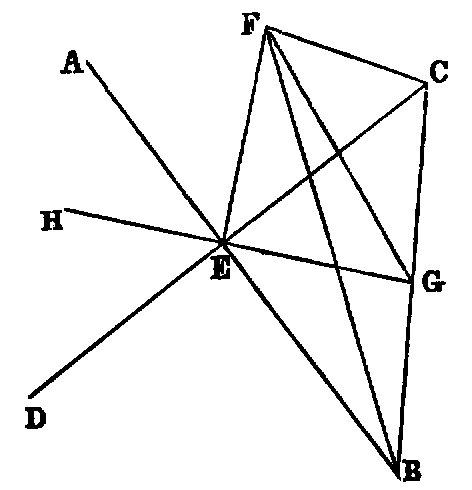
Dem.—Through any point G in GH draw a line BC intersecting AB, CD, and so as to be bisected in G; and join any point F in EF to B, G, C. Then, because EF is perpendicular to the lines EB, EC, we have

	BF2 = BE2 + EF2, and CF2 = CE2 + EF2;
		∴ BF2 + CF2	= BE2 + CE2 + 2EF2.
	Again	BF2 + CF2	= 2BG2 + 2GF2 [II. x. Ex. 2],
	and	BE2 + CE2	= 2BG2 + 2GE2;
		∴ 2BG2 + 2GF2	= 2BG2 + 2GE2 + 2EF2;
		∴ GF2	= GE2 + EF2.

Hence the angle GEF is right, and EF is perpendicular to EG.

Def. vi.—A line such as EF, which is perpendicular to a system of concurrent and coplanar lines, is said to be perpendicular to the plane of these lines, and is called a normal to it.

Cor. 1.—The normal is the least line that may be drawn from a given point to a given plane; and of all others that may be drawn to it, the lines of any system making equal angles with the normal are equal to each other.

Cor. 2.—A perpendicular to each of two intersecting lines is normal to their plane.

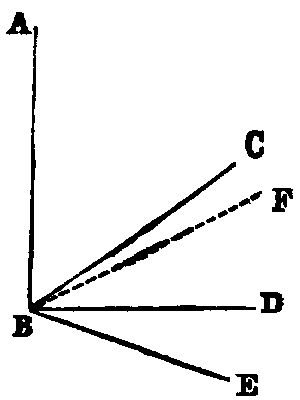
If three concurrent lines (BC, BD, BE) have a common perpendicular (AB), they are coplanar.

Dem.—For if possible let BC be not coplanar with BD, BE, and let the plane of AB, BC intersect the plane of BD, BE in the line BF. Then [XI. iii.] BF is a right line; and, since it is coplanar with BD, BE, which are each perpendicular to AB, it is [XI. iv.] perpendicular to AB. Therefore the angle ABF is right; and the angle ABC is right (hyp.). Hence ABC is equal to ABF, which is impossible [I., Axiom ix.]. Therefore the lines BC, BD, BE are coplanar.

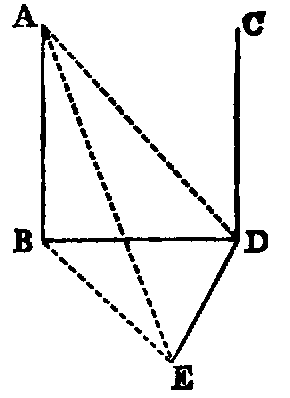
Dem.—Let AB, CD meet the plane X at the points B, D. Join BD, and in the plane X draw DE at right angles to BD; take any point E in DE. Join BE, AE, AD. Then because AB is normal to X, the angle ABE is right. Therefore AE² = AB² + BE² = AB² + BD² + DE²; because the angle BDE is right. But AB² + BD² = AD², because the angle ABD is right. Hence AE² = AD² + DE². Therefore the angle ADE is right. [I. xlviii]. And since CD is normal to the plane X, DE is perpendicular to CD. Hence DE is a common perpendicular to the three concurrent lines CD, AD, BD. Therefore these lines are coplanar [XI. v.]. But AB is coplanar with AD, BD [XI. ii.]. Therefore the lines AD, BD, CD are coplanar; and since the angles ABD, BDC are right, the line AB is parallel to CD [I. xxviii.].

Def. vii.—If from every point in a given line normals be drawn to a given plane, the locus of their feet is called the projection of the given line on the plane.

1. The projection of any line on a plane is a right line.

2. The projection on either of two intersecting planes of a normal to the other plane is perpendicular to the line of intersection of the planes.

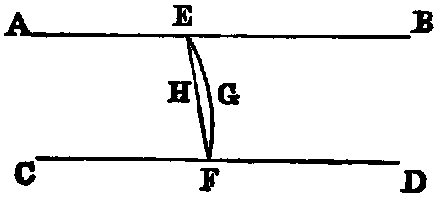
Dem.—If possible let the intersecting line be out of the plane, as EGF. And in the plane, of the parallels draw [I. Post. ii.] the right line EHF. Then we have two right lines EGF, EHF, enclosing a space, which [I. Axiom x.] is impossible. Hence the two parallel right lines and the transversal are coplanar.

Or thus: Since the points E, F are in the plane of the parallels, the line joining these points is in that plane [I. Def. vi].

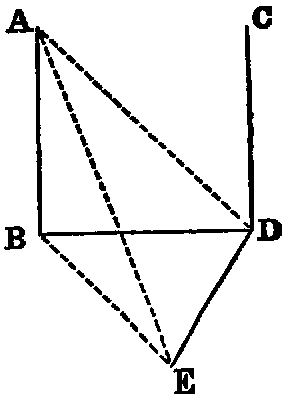
Dem.—Let AB, CD meet the plane X in the points B, D. Join BD. Then the lines AB, BD, CD are coplanar. Now in the plane X, to which AB is normal, draw DE at right angles to BD. Take any point E in DE, and join BE, AE, AD.

Then because AB is normal to the plane X, it is perpendicular to the line BE in that plane [XI. Def. vi.]. Hence the angle ABE is right; therefore AE² = AB² + BE² = AB² + BD² + DE² (because BDE is right (const.)) = AD² + DE² (because ABD is right (hyp.)). Therefore the angle ADE is right. Hence DE is at right angles both to AD and BD. Therefore [XI. iv.] DE is perpendicular to CD, which is coplanar and concurrent with AD and BD. Again, since AB and CD are parallel, the sum of the angles ABD, BDC is two right angles [I. xxix.]; but ABD is right (hyp.); therefore BDC is right. Hence CD is perpendicular to the two lines DB, DE, and therefore [XI. iv.] it is normal to their plane, that is, it is normal to X.

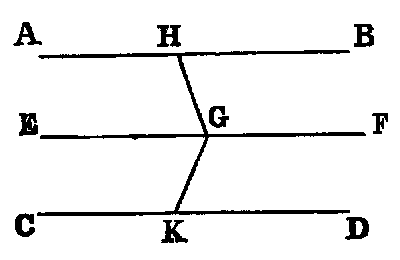
Dem.—If the three lines be coplanar, the Proposition is evidently the same as I. xxx. If they are not coplanar, from any point G in EF draw in the planes of EF, AB; EF, CD, respectively, the lines GH, GK each perpendicular to EF [I. xi.]. Then because EF is perpendicular to each of the lines GH, GK, it is normal to their plane [XI. iv.]. And because AB is parallel to EF (hyp.), and EF is normal to the plane GHK, AB is normal to the plane GHK [XI. viii.]. In like manner CD is normal to the plane HGK. Hence, since AB and CD are normals to the same plane, they are parallel to one another.

If two intersecting right lines (AB, BC) be respectively parallel to two other intersecting right lines (DE, EF), the angle (ABC) between the former is equal to the angle (DEF) between the latter.

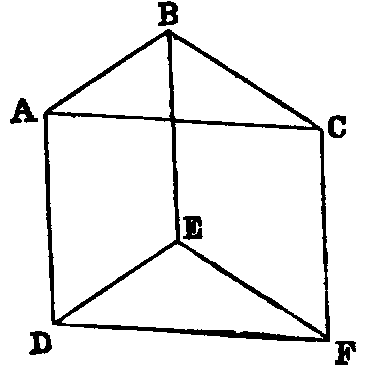
Dem.—If both pairs of lines be coplanar, the proposition is the same as I. xxix., Ex. 2. If not, take any points A, C in the lines AB, BC, and cut off ED = BA, and EF = BC [I. iii.]. Join AD, BE, CF, AC, DF. Then because AB is equal and parallel to DE, AD is equal and parallel to BE [I. xxxiii]. In like manner CF is equal and parallel to BE. Hence [XI. ix.] AD is equal and parallel to CF. Hence [I. xxxiii.] AC is equal to DF. Therefore the triangles ABC, DEF, have the three sides of one respectively equal to the three sides of the other. Hence [I. viii.] the angle ABC is equal to DEF.

Def. viii.—Two planes which meet are perpendicular to each other, when the right lines drawn in one of them perpendicular to their common section are normals to the other.

Def. ix.—When two planes which meet are not perpendicular to each other, their inclination is the acute angle contained by two right lines drawn from any point of their common section at right angles to it—one in one plane, and the other in the other.

Observation.—These definitions tacitly assume the result of Props. iii. and x. of this book. On this account we have departed from the usual custom of placing them at the beginning of the book. We have altered the place of Definition vi. for a similar reason.

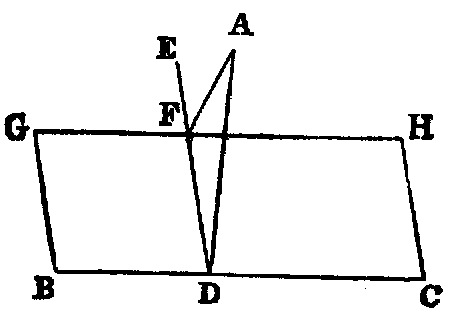
Sol.—In the given plane BH draw any line BC, and from A draw AD perpendicular to BC [I. xii.]; then if AD be perpendicular to the plane, the thing required is done. If not, from D draw DE in the plane BH at right angles to BC [I. xi.], and from A draw AF [I. xii.] perpendicular to DE. AF is normal to the plane BH.

Dem.—Draw GH parallel to BC. Then because BC is perpendicular both to ED and DA, it is normal to the plane of ED, DA [XI. iv.]; and since GH is parallel to BC, it is normal to the same plane [XI. viii.]. Hence AF is perpendicular to GH [XI. Def. vi.], and AF is perpendicular to DE (const.). Therefore AF is normal to the plane of GH and ED—that is, to the plane BH.

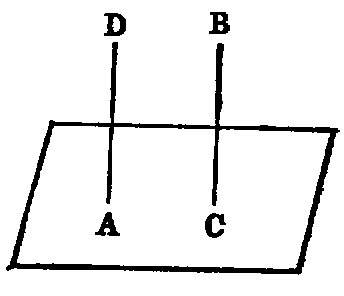
To draw a normal to a given plane from a given point (A) in the plane.

Sol.—From any point B not in the plane draw [XI. xi.] BC normal to it. If this line pass through A it is the normal required. If not, from A draw AD parallel to BC [I. xxxi.]. Then because AD and BC are parallel, and BC is normal to the plane, AD is also normal to it [XI. viii.], and it is drawn from the given point. Hence it is the required normal.

From the same point (A) there can be but one normal drawn to a given plane (X).

Dem.—1. Let A be in the given plane, and if possible let AB, AC be both normals to it, on the same side. Now let the plane of BA, AC cut the given plane X in the line DE. Then because BA is a normal, the angle BAE is right. In like manner CAE is right. Hence BAE = CAE, which is impossible.

2. If the point be above the plane, there can be but one normal; for, if there could be two, they would be parallel [XI. vi.] to one another, which is absurd. Therefore from the same point there can be drawn but one normal to a given plane.

Planes (CD, EF) which have a common normal (AB) are parallel to each other.

Dem.—If the planes be not parallel, they will meet when produced. Let them meet, their common section being the line GH, in which take any point K. Join AK, BK. Then because AB is normal to the plane CD, it is perpendicular to the line AK, which it meets in that plane [XI. Def. vi.]. Therefore the angle BAK is right. In like manner the angle ABK is right. Hence the plane triangle ABK has two right angles, which is impossible. Therefore the planes CD, EF cannot meet—that is, they are parallel.

1. The angle between two planes is equal to the angle between two intersecting normals to these planes.

2. If a line be parallel to each of two planes, the sections which any plane passing through it makes with them are parallel.

3. If a line be parallel to each of two intersecting planes, it is parallel to their intersection.

4. If two right lines be parallel, they are parallel to the common section of any two planes passing through them.

5. If the intersections of several planes be parallel, the normals drawn to them from any point are coplanar.