Contents

Geometry is the Science of figured Space. Figured Space is of one, two, or three dimensions, according as it consists of lines, surfaces, or solids. The boundaries of solids are surfaces; of surfaces, lines; and of lines, points. Thus it is the province of Geometry to investigate the properties of solids, of surfaces, and of the figures described on surfaces. The simplest of all surfaces is the plane, and that department of Geometry which is occupied with the lines and curves drawn on a plane is called Plane Geometry; that which demonstrates the properties of solids, of curved surfaces, and the figures described on curved surfaces, is Geometry of Three Dimensions. The simplest lines that can be drawn on a plane are the right line and circle, and the study of the properties of the point, the right line, and the circle, is the introduction to Geometry, of which it forms an extensive and important department. This is the part of Geometry on which the oldest Mathematical Book in existence, namely, Euclid’s Elements, is written, and is the subject of the present volume. The conic sections and other curves that can be described on a plane form special branches, and complete the divisions of this, the most comprehensive of all the Sciences. The student will find in Chasles’ Aperçu Historique a valuable history of the origin and the development of the methods of Geometry.

In the following work, when figures are not drawn, the student should construct them from the given directions. The Propositions of Euclid will be printed in larger type, and will be referred to by Roman numerals enclosed in brackets. Thus [III. xxxii.] will denote the 32nd Proposition of the 3rd Book. The number of the Book will be given only when different from that under which the reference occurs. The general and the particular enunciation of every Proposition will be given in one. By omitting the letters enclosed in parentheses we have the general enunciation, and by reading them, the particular. The annotations will be printed in smaller type. The following symbols will be used in them:—

Circle	will be denoted by	⊙
Triangle	,,	△
Parallelogram	,,
Parallel lines	,,	∥
Perpendicular	,,	⊥

In addition to these we shall employ the usual symbols +, −, &c. of Algebra, and also the sign of congruence, namely ≡. This symbol has been introduced by the illustrious Gauss.

i. A point is that which has position but not dimensions.

A geometrical magnitude which has three dimensions, that is, length, breadth, and thickness, is a solid; that which has two dimensions, such as length and breadth, is a surface; and that which has but one dimension is a line. But a point is neither a solid, nor a surface, nor a line; hence it has no dimensions—that is, it has neither length, breadth, nor thickness.

ii. A line is length without breadth.

A line is space of one dimension. If it had any breadth, no matter how small, it would be space of two dimensions; and if in addition it had any thickness it would be space of three dimensions; hence a line has neither breadth nor thickness.

iii. The intersections of lines and their extremities are points.

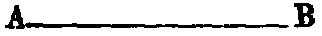
iv. A line which lies evenly between its extreme points is called a straight or right line, such as AB.

If a point move without changing its direction it will describe a right line. The direction in which a point moves in called its “sense.” If the moving point continually changes its direction it will describe a curve; hence it follows that only one right line can be drawn between two points. The following Illustration is due to Professor Henrici:—“If we suspend a weight by a string, the string becomes stretched, and we say it is straight, by which we mean to express that it has assumed a peculiar definite shape. If we mentally abstract from this string all thickness, we obtain the notion of the simplest of all lines, which we call a straight line.”

v. A surface is that which has length and breadth.

A surface is space of two dimensions. It has no thickness, for if it had any, however small, it would be space of three dimensions.

vi. When a surface is such that the right line joining any two arbitrary points in it lies wholly in the surface, it is called a plane.

A plane is perfectly flat and even, like the surface of still water, or of a smooth floor.—Newcomb.

vii. Any combination of points, of lines, or of points and lines in a plane, is called a plane figure. If a figure be formed of points only it is called a stigmatic figure; and if of right lines only, a rectilineal figure.

viii. Points which lie on the same right line are called collinear points. A figure formed of collinear points is called a row of points.

ix. The inclination of two right lines extending out from one point in different directions is called a rectilineal angle.

x. The two lines are called the legs, and the point the vertex of the angle.

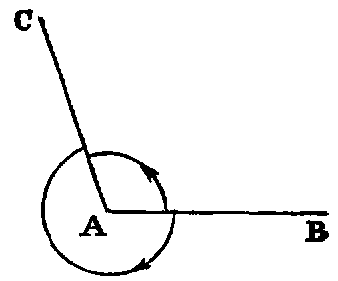
A right line drawn from the vertex and turning about it in the plane of the angle, from the position of coincidence with one leg to that of coincidence with the other, is said to turn through the angle, and the angle is the greater as the quantity of turning is the greater. Again, since the line may turn from one position to the other in either of two ways, two angles are formed by two lines drawn from a point.

Thus if AB, AC be the legs, a line may turn from the position AB to the position AC in the two ways indicated by the arrows. The smaller of the angles thus formed is to be understood as the angle contained by the lines. The larger, called a re-entrant angle, seldom occurs in the “Elements.”

xi. Designation of Angles.—A particular angle in a figure is denoted by three letters, as BAC, of which the middle one, A, is at the vertex, and the other two along the legs. The angle is then read BAC.

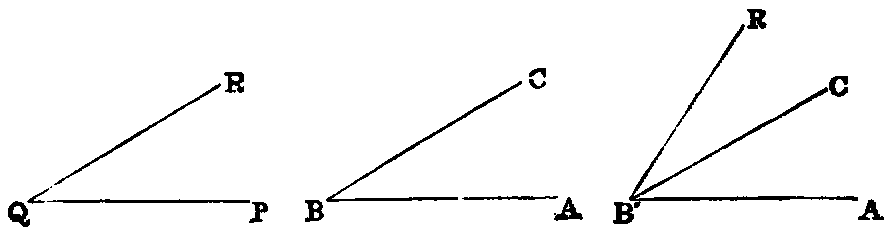
xii. The angle formed by joining two or more angles together is called their sum. Thus the sum of the two angles ABC, PQR is the angle AB′R,

formed by applying the side QP to the side BC, so that the vertex Q shall fall on the vertex B, and the side QR on the opposite side of BC from BA.

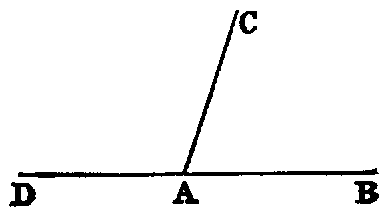
xiii. When the sum of two angles BAC, CAD is such that the legs BA, AD form one right line, they are called supplements of each other.

Hence, when one line stands on another, the two angles which it makes on the same side of that on which it stands are supplements of each other.

xiv. When one line stands on another, and makes the adjacent angles at both sides of itself equal, each of the angles is called a right angle, and the line which stands on the other is called a perpendicular to it.

Hence a right angle is equal to its supplement.

xv. An acute angle is one which is less than a right angle, as A.

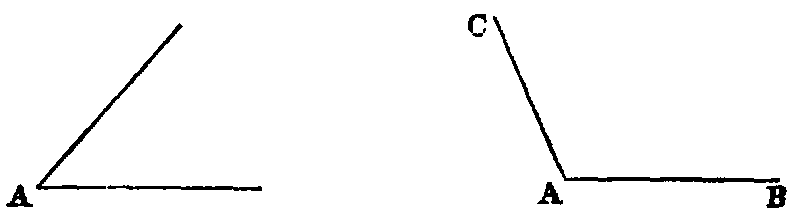
xvi. An obtuse angle is one which is greater than a right angle, as BAC.

The supplement of an acute angle is obtuse, and conversely, the supplement of an obtuse angle is acute.

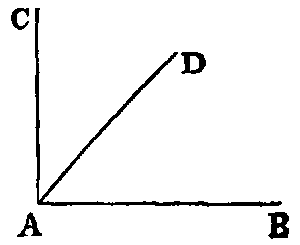
xvii. When the sum of two angles is a right angle, each is called the complement of the other. Thus, if the angle BAC be right, the angles BAD, DAC are complements of each other.

xviii. Three or more right lines passing through the same point are called concurrent lines.

xix. A system of more than three concurrent lines is called a pencil of lines. Each line of a pencil is called a ray, and the common point through which the rays pass is called the vertex.

xx. A triangle is a figure formed by three right lines joined end to end. The three lines are called its sides.

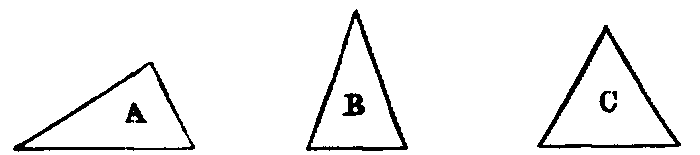
xxi. A triangle whose three sides are unequal is said to be scalene, as A; a triangle having two sides equal, to be isosceles, as B; and and having all its sides equal, to be equilateral, as C.

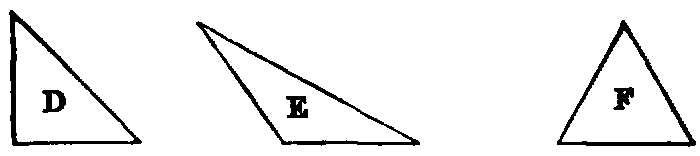
xxii. A right-angled triangle is one that has one of its angles a right angle, as D. The side which subtends the right angle is called the hypotenuse.

xxiii. An obtuse-angled triangle is one that has one of its angles obtuse, as E.

xxiv. An acute-angled triangle is one that has its three angles acute, as F.

xxv. An exterior angle of a triangle is one that is formed by any side and the continuation of another side.

Hence a triangle has six exterior angles; and also each exterior angle is the supplement of the adjacent interior angle.

xxvi. A rectilineal figure bounded by more than three right lines is usually called a polygon.

xxvii. A polygon is said to be convex when it has no re-entrant angle.

xxviii. A polygon of four sides is called a quadrilateral.

xxix. A quadrilateral whose four sides are equal is called a lozenge.

xxx. A lozenge which has a right angle is called a square.

xxxi. A polygon which has five sides is called a pentagon; one which has six sides, a hexagon, and so on.

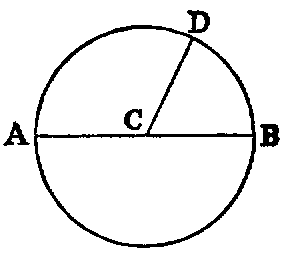
xxxii. A circle is a plane figure formed by a curved line called the circumference, and is such that all right lines drawn from a certain point within the figure to the circumference are equal to one another. This point is called the centre.

xxxiii. A radius of a circle is any right line drawn from the centre to the circumference, such as CD.

xxxiv. A diameter of a circle is a right line drawn through the centre and terminated both ways by the circumference, such as AB.

From the definition of a circle it follows at once that the path of a movable point in a plane which remains at a constant distance from a fixed point is a circle; also that any point P in the plane is inside, outside, or on the circumference of a circle according as its distance from the centre is less than, greater than, or equal to, the radius.

Let it be granted that—

i. A right line may be drawn from any one point to any other point.

When we consider a straight line contained between two fixed points which are its ends, such a portion is called a finite straight line.

ii. A terminated right line may be produced to any length in a right line.

Every right line may extend without limit in either direction or in both. It is in these cases called an indefinite line. By this postulate a finite right line may be supposed to be produced, whenever we please, into an indefinite right line.

iii. A circle may be described from any centre, and with any distance from that centre as radius.

If there be two points A and B, and if with any instruments, such as a ruler and pen, we draw a line from A to B, this will evidently have some irregularities, and also some breadth and thickness. Hence it will not be a geometrical line no matter how nearly it may approach to one. This is the reason that Euclid postulates the drawing of a right line from one point to another. For if it could be accurately done there would be no need for his asking us to let it be granted. Similar observations apply to the other postulates. It is also worthy of remark that Euclid never takes for granted the doing of anything for which a geometrical construction, founded on other problems or on the foregoing postulates, can be given.

i. Things which are equal to the same, or to equals, are equal to each other.

Thus, if there be three things, and if the first, and the second, be each equal to the third, we infer by this axiom that the first is equal to the second. This axiom relates to all kinds of magnitude. The same is true of Axioms ii., iii., iv., v., vi., vii., ix.; but viii., x., xi., xii., are strictly geometrical.

ii. If equals be added to equals the sums will be equal.

iii. If equals be taken from equals the remainders will be equal.

iv. If equals be added to unequals the sums will be unequal.

v. If equals be taken from unequals the remainders will be unequal.

vi. The doubles of equal magnitudes are equal.

vii. The halves of equal magnitudes are equal.

viii. Magnitudes that can be made to coincide are equal.

The placing of one geometrical magnitude on another, such as a line on a line, a triangle on a triangle, or a circle on a circle, &c., is called superposition. The superposition employed in Geometry is only mental, that is, we conceive one magnitude placed on the other; and then, if we can prove that they coincide, we infer, by the present axiom, that they are equal. Superposition involves the following principle, of which, without explicitly stating it, Euclid makes frequent use:—“Any figure may be transferred from one position to another without change of form or size.”

ix. The whole is greater than its part.

This axiom is included in the following, which is a fuller statement:—

ix′. The whole is equal to the sum of all its parts.

x. Two right lines cannot enclose a space.

This is equivalent to the statement, “If two right lines have two points common to both, they coincide in direction,” that is, they form but one line, and this holds true even when one of the points is at infinity.

xi. All right angles are equal to one another.

This can be proved as follows:—Let there be two right lines AB, CD, and two perpendiculars to them, namely, EF, GH, then if AB, CD be made to coincide by superposition, so that the point E will coincide with G; then since a right angle is equal to its supplement, the line EF must coincide with GH. Hence the angle AEF is equal to CGH.

xii. If two right lines (AB, CD) meet a third line (AC), so as to make the sum of the two interior angles (BAC, ACD) on the same side less than two right angles, these lines being produced shall meet at some finite distance.

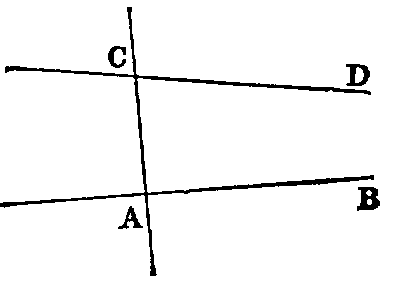
This axiom is the converse of Prop. xvii., Book I.

Axioms.—“Elements of human reason,” according to Dugald Stewart, are certain general propositions, the truths of which are self-evident, and which are so fundamental, that they cannot be inferred from any propositions which are more elementary; in other words, they are incapable of demonstration. “That two sides of a triangle are greater than the third” is, perhaps, self-evident; but it is not an axiom, inasmuch as it can be inferred by demonstration from other propositions; but we can give no proof of the proposition that “things which are equal to the same are equal to one another,” and, being self-evident, it is an axiom.

Propositions which are not axioms are properties of figures obtained by processes of reasoning. They are divided into theorems and problems.

A Theorem is the formal statement of a property that may be demonstrated from known propositions. These propositions may themselves be theorems or axioms. A theorem consists of two parts, the hypothesis, or that which is assumed, and the conclusion, or that which is asserted to follow therefrom. Thus, in the typical theorem,

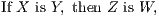
the hypothesis is that X is Y , and the conclusion is that Z is W.

Converse Theorems.—Two theorems are said to be converse, each of the other, when the hypothesis of either is the conclusion of the other. Thus the converse of the theorem (i.) is—

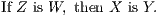
From the two theorems (i.) and (ii.) we may infer two others, called their contrapositives. Thus the contrapositive

The theorem (iv.) is called the obverse of (i.), and (iii.) the obverse of (ii.).

A Problem is a proposition in which something is proposed to be done, such as a line to be drawn, or a figure to be constructed, under some given conditions.

The Solution of a problem is the method of construction which accomplishes the required end.

The Demonstration is the proof, in the case of a theorem, that the conclusion follows from the hypothesis; and in the case of a problem, that the construction accomplishes the object proposed.

The Enunciation of a problem consists of two parts, namely, the data, or things supposed to be given, and the quaesita, or things required to be done.

Postulates are the elements of geometrical construction, and occupy the same relation with respect to problems as axioms do to theorems.

A Corollary is an inference or deduction from a proposition.

A Lemma is an auxiliary proposition required in the demonstration of a principal proposition.

A Secant or Transversal is a line which cuts a system of lines, a circle, or any other geometrical figure.

Congruent figures are those that can be made to coincide by superposition. They agree in shape and size, but differ in position. Hence it follows, by Axiom viii., that corresponding parts or portions of congruent figures are congruent, and that congruent figures are equal in every respect.

Rule of Identity.—Under this name the following principle will be sometimes referred to:—“If there is but one X and one Y , then, from the fact that X is Y , it necessarily follows that Y is X.”—Syllabus.