Process Capability
Introduction:
Process capability (PC) is the study which needs to be undertaken to determine whether the process is stable and whether it will remain stable. Process capability therefore is the ability of the process to meet customer requirements.
Definition:
It has been defined as follows:"
'PC is the results of which the process is capable under stable conditions; it is, in essence, a prediction developed through the application of statistical theory as to whether a process is capable of meeting the specification limits necessary to fulfill the requirements of the product design.'
Process capability therefore is the ability of the process to meet customer requirements again and again by asking the following questions:
- How stable is the process? Could we predict its performance again and again?
- Could we control its performance by changing requirements? Process capability has to be looked at from two different angles;
- Inherent capability: the amount of variation which is existing in the process output;
- Determined capability through specifications: This is determined by selecting a standard (nominal) value and some tolerances. Process capability is usually predicted within or - 3 standard deviations of the data from the mean representing 6a or 99.74% of probable occurrences.
The Cp index:
The Cp index measures the process potential by assessing whether the natural tolerance (6a) is within the specification limits.
Cp = USL - LSL/6a
A Cp of 1 is considered as adequate and exactly the same as the total tolerance width.
If Cp < 1 the process lacks potential to meet specified requirements;
If Cp > 1 the process may have the potential to meet customer requirements
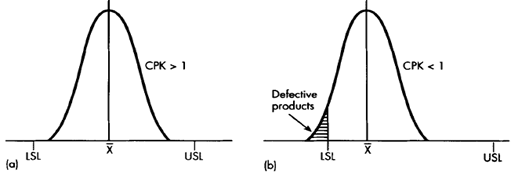
The Cp index only looks at potential process performance by mainly concentrating on the spread of the process rather than its location. This is why another index is required.
The Cpk index:
The Cpk uses the process mean to measure constantly the distance between the process mean and the upper and lower specification limits.
The Cpk is calculated as follows:
Cpk = lesser value of (USL - m3, or X - LSL/3a)
The higher the value of the Cpk the more this is indicative of process capability.
To highlight the difference between the Cp and the Cpk, is acceptable because the Cpk is > 1. However, may be acceptable under the Cp index because it looks at the spread of the process under the specified limits. As the example shows this is not acceptable however, since the process settings have been changed, and the process requires new specifications.