Statistical Learning

In both Bayesian learning and MAP learning, the hypothesis prior P(hi) plays an important role. We saw in Chapter 18 that overfitting can occur when the hypothesis space is too expressive, so that it contains many hypotheses that fit the data set well. Rather than placing an arbitrary limit on the hypotheses to be considered, Bayesian and MAP learning methods use the prior to penalize complexity. Typically, more complex hypotheses have a lower prior probability—in part because there are usually many more complex hypotheses than simple hypotheses. On the other hand, more complex hypotheses have a greater capacity to fit the data. (In the extreme case, a lookup table can reproduce the data exactly with probability 1.) Hence, the hypothesis prior embodies a trade-off between the complexity of a hypothesis and its degree of fit to the data.
We can see the effect of this trade-off most clearly in the logical case, where H contains only deterministic hypotheses. In that case, P(djhi) is 1 if hi is consistent and 0 otherwise. Looking at Equation (20.1), we see that hMAP will then be the simplest logical theory that is consistent with the data. Therefore, maximum a posteriori learning provides a natural embodiment of Ockham’s razor.
Another insight into the trade-off between complexity and degree of fit is obtained by taking the logarithm of Equation (20.1). Choosing hMAP to maximize P(dlhi)P(hi) is equivalent to minimizing
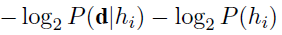
Using the connection between information encoding and probability, we see that the _ log2 P(hi) term equals the number of bits required to specify the hypothesis hi. Furthermore, _log2 P(djhi) is the additional number of bits required to specify the data, given the hypothesis. (To see this, consider that no bits are required if the hypothesis predicts the data exactly—as with h5 and the string of lime candies—and log2 1=0.) Hence, MAP learning is choosing the hypothesis that provides maximum compression of the data. The same task is addressed more directly by the minimum description length, or MDL, learning method, which attempts to minimize the size of hypothesis and data encodings rather than work with probabilities.
A final simplification is provided by assuming a uniform prior over the space of hypotheses. In that case, MAP learning reduces to choosing an hi that maximizes P(djHi). This is called a maximum-likelihood (ML) hypothesis, hML MAXIMUM . Maximum-likelihood learning is very common in statistics, a discipline in which many researchers distrust the subjective nature of hypothesis priors. It is a reasonable approach when there is no reason to prefer one hypothesis over another a priori—for example, when all hypotheses are equally complex. It provides a good approximation to Bayesian and MAP learning when the data set is large, because the data swamps the prior distribution over hypotheses, but it has problems (as we shall see) with small data sets.