A Taxonomy Of Formal Languages And Machines
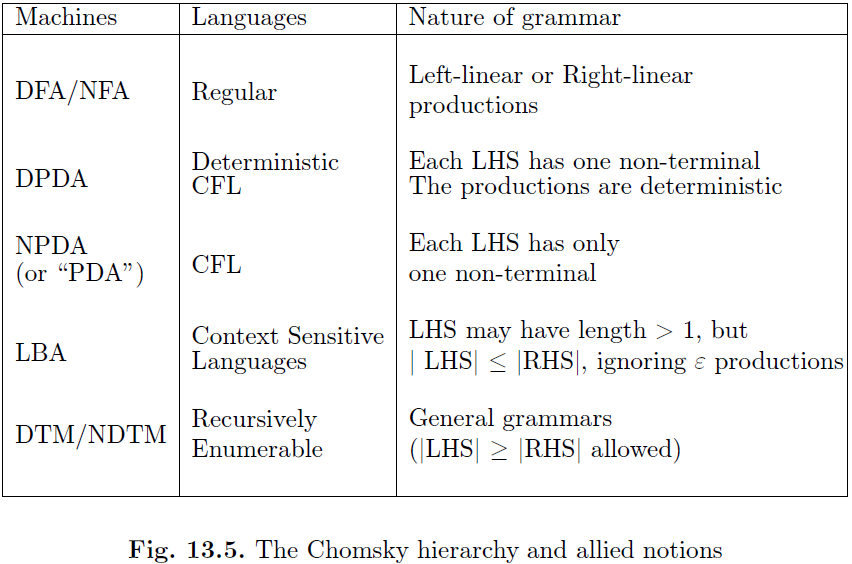
We now summarize the formal machines, as well as languages, studied in this book in the table given in Figure 13.5. This is known as the Chomsky hierarchy of formal languages. For each machine, we describe the nature of its languages, and indicate the nature of the grammar used to describe the languages. It is interesting that simply by varying the nature of production rules, we can obtain all members of the Chomsky hierarchy. This single table, in a sense, summarizes some of the main achievements of over 50 years of research in computability, machines, automata, and grammars. Here is a summary of the salient points made in this table, listed against each of the language classes:2
Regular languages: DFAs and NFAs serve as machines that recognize regular languages. Context-free grammars written with only left-linear or only right-linear productions can generate or recognize regular languages. The linearity of the production rules means that there is only one non-terminal allowed on the RHS of each production, which appears leftmost or rightmost. Hence, these non-terminals can be regarded as states of an NFA.
Deterministic context-free languages (DCFL): Push-down automata are machines that recognize DCFLs, as illustrated in Illustration 13.4.2. In effect, they can parse sentences in the language without backtracking (deterministically). As for grammars, the fact that each context-free production specifies the expansion of
one and only one non-terminal on the left-hand side means that this expansion is good wherever the non-terminal appears—i.e., regardless of the context (hence “context-free”). The grammars are deterministic.
Context-free languages (CFL): These are more general than DCFLs, as the constraint of determinism is removed in the underlying machines and grammars.
Context-sensitive languages (CSL): CSLs can be recognized by linear bounded automata which are described in Section 15.2.3. Basically, they are restricted Turing machines which can write only on that portion of the input tape on which the input was originally laid out. In particular, given any LBA M and a string w, it can be conclusively answered as to whether M accepts w or not. This is impossible with a Turing machine. As for grammars, CSLs are recognized by productions in which the length of a left-hand side is allowed to be more than 1. Such a contextsensitive production specifies a pattern on the LHS, and a sentential form on the RHS. In a sense, we can have a rule of the form a A d -> a a c d and another of the form a A e -> a c a d. Notice that A’s expansion when surrounded by a and d can be different from when surrounded by a and e, thus building in context sensitivity to the interpretation of A. The length of the RHS is required to be no less than that of the LHS (except in the ε case) to ensure decidability in some cases.
Recursively enumerable or Turing recognizable (RE or TR) languages: These form the most general language class in the Chomsky hierarchy. Notice that Turing machines as well as unrestricted productions, form the machines and grammars for this language class.
CFGs and CFLs are fundamental to computer science because they help describe the structure underlying programming languages. The basic “signature” of a CFL is “nested brackets:” for example, nesting occurs in expressions and in very many statically scoped structures in computer programs. In contrast, the basic signature of regular languages is “iteration (looping) according to some ultimate periodicity.” Illustration 13.4.1 Let us argue that the programming language C is not regular. Let there be a DFA for C with n states. Now consider the C program
CNOP = {main(){n}n | n ≥ 0}.
Clearly, the DFA for C will loop in the part described by main(){n, and by pumping this region wherever the loop might fall, we will obtain a malformed C program. Some of the pumps could, for instance, result in the C program maiaiain(){. . ., while some others result in strings of the form main{{{}}, etc. Using a CFG, we can describe CNOP using production rules, as follows:
L_C_nop -> main Paren Braces
Paren -> ()
Braces -> epsilon | { Braces }.