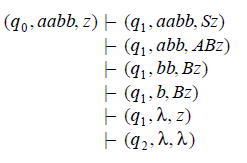Cfg To Npda

CFG to NPDA: For any context-free grammar in GNF, it is easy to build an equivalent nondeterministic pushdown automaton (NPDA).

Any string of a context-free language has a leftmost derivation. We set up the NPDA so that the stack contents “corresponds” to this sentential form: every move of the NPDA represents one derivation step.

The sentential form is

(The char acters already read) (sym bols on the stack)– (Final z (ini tial stack sym bol)

In the NPDA, we will construct, the states that are not of much importance. All the real work is done on the stack. We will use only the following three states, irrespective of the complexity of the grammar.

(i) start state q0 just gets things initialized. We use the transition from q0 to q1 to put the grammar’s start symbol on the stack.

d(q0 , l, Z) -> {(q1 , Sz)}

(ii) State q1 does the bulk of the work. We represent every derivation step as a move from q1 to q1.

(iii) We use the transition from q1 to qf to accept the string

d(q1 , l, z) -> {(q f , z)}

ExampleConsider the grammar G = ({S, A, B},{a, b}, S, P), where

P = {S -> a, S -> aAB, A-> aA, A-> a, B-> bB, B-> b}

These productions can be turned into transition functions by rearranging the components.

For example, the derivation

S =>aAB =>aaB =>aabB =>aabb

maps into the sequence of moves