Exampleof Non Deterministic Finite Automata

Example of a NFA, Nondeterministic Finite Automata givenby

1. Machine Definition  M = (Q, sigma, delta, q0, F)
2. Equivalent regular expression
3. Equivalent state transition diagramand example tree of states for input string 0100011and an equivalent DFA, Deterministic Finite Automata for thefirst 3 states.

a) Machine DefinitionM = (Q, sigma, delta, q0, F)

Q = { q0, q1, q2, q3, q4 } the set of states

sigma = { 0, 1 }           the input string alphabet

delta                      the state transition table

 q0 = q0                    the starting state

 F = { q2, q4 }             the set of final states (accepting when in

this state and no more input)

inputs

delta    |    0    |    1    |

         --------- --------- ---------

q0  | {q0,q3} | {q0,q1} |

q1  |   phi   |   {q2}  |

states    q2  |   {q2}  |   {q2}  |

q3  |   {q4}  |   phi   |

q4  |   {q4}  |   {q4}  |

 ^       ^         ^

|       |         |

|       --------- -- a set of states, phi means empty set

              -- every state must be listed

b) The equivalent regular expression is  (0 1)*(00 11)(0 1)*  This NFA represents the language L = all strings over {0,1} that have at least two consecutive 0's or 1's.

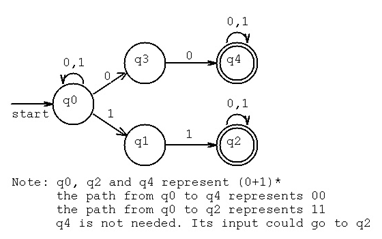
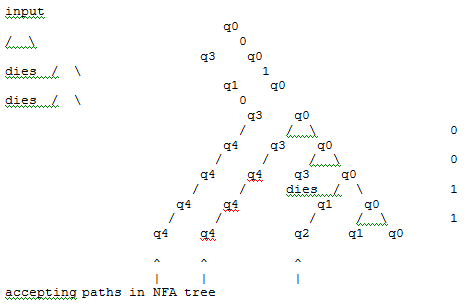
c) Equivalent NFA state transition diagram.: Note that state q3 does not go anywhere for an input of 1. We use the terminology that the path "dies" if in q3 getting an input 1. The tree of states this NFA is in for the input  0100011