Graphs

Introduction: An undirected graph or simply a graph is a set of points with lines connecting some points. The points are called nodes or vertices. The lines are called edges.

Types of graphs:

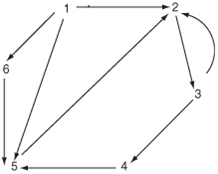
1.       The number of edges at a particular vertex is the degree of the vertex. In Figure 1, degree of 1 is 3. No more than one edge is allowed between any two vertices. We label the vertices for convenience, and call the graph as labeled graph.

2.       An undirected graph:  is connected if every pair of vertices is connected by a path. A path in a graph is a contiguous sequence of its vertices.

• In any graph G, a path forms a cycle if its starting vertex and end vertex are same.
• A connected, acyclic, undirected graph is a tree.

3.       A directed graphhas directed lines between the nodes. The number of arrows pointing from a particular node is the out degree of that node and the number of arrows to a particular node is the in degree.

4.       A rooted treeis a tree in which one of the vertices is distinguished from others. Such a vertex is called the root of the tree.

Figure 1:Examples of undirected graphs:The number of edges at a particular vertex is the degree of the vertex. In Figure 1.1, degree of 1 is 3. No more than one edge is allowed between any two vertices. We label the vertices for convenience, and call the graph as labeled graph.

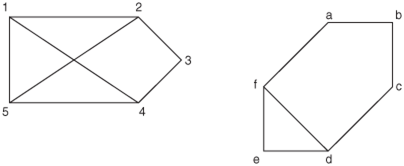
An induced subgraph H of a graph G is a graph with nodes of H being a subset of the nodes of G, and edges of H being the edges of G on the corresponding nodes. A path in a graph is a sequence of nodes connected by edges. A simple path is a path that does not repeat any node. A graph is connected if any two nodes have a path between them. A path is a cycle if it starts and ends in the same node. A simple cycle is one that does not repeat any node except the first and the last. A tree graph is a connected graph that has no simple cycle. The nodes of degree 1 in a tree are called the leaves of the tree.

Figure 2: An example of a directed graph: In the following directed graph (Figure 1.2) the indegree of node labeled 2 is 3 and its outdegree is 1.