Programming A Turing Machine

Programming a Turing Machine: As we have the “productions” as the control theme of a grammar, the “transitions” are the central theme of a Turing machine. These transitions are given as a table or list of S-tuples, where each tuple has the form (current state, sym bol read, sym bol writ ten, direc tion, next state)

Creating such a list is called “programming” a Turing machine.

A Turing machine is often defined to start with the read head positioned over the first (leftmost) input symbol. This is not really necessary, because if the Turing machine starts anywhere on the nonblank portion of the tape, it is simple to get to the first input symbol.

For the input alphabet S = {a, b}, the following program fragment does the trick, then goes to state q1.

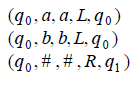
Turing Machines as Acceptors: A Turing machine halts when it no longer has available moves. If it halts in a final state, it accepts its input, otherwise it rejects its input.

A Turing machine T = (Q, S,G,d, q , # , F ) 0 accepts a language L(M), where

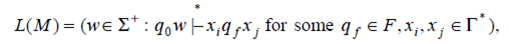
with the assumption that the Turing machine starts with its tape head positioned on the leftmost symbol.

A Turing Machine accepts its input if it halts in a final state. There are two ways this could fail to happen:

(a)    The Turing machine could halt in a nonfinal state or

(b)    The Turing machine could never stop i.e., it enters an “infinite loop”.

How to Recognize a Language: This machine will match strings of the form

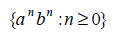
q1 is the only “final state”.

q4 (which has no available moves at all) serves as an “error state”.