Usage Of Pumping Lemma
Usage of Pumping Lemma: The Pumping Lemma can be used to show that certain languages are not context free.
Let us show that the language
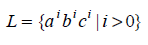
is not context-free.
Proof:Suppose L is a context-free language.
If string X ∈L, where| X | > m, it follows that X = uvwxy, where| vwx| £ m. Choose a value i that is greater than m. Then, wherever vwx occurs in the string a ibici , it cannot contain more than two distinct letters it can be all a’s, all b’s, all c’s, or it can be a’s and b’s, or it can be b’s and c’s.
Therefore the string vx cannot contain more than two distinct letters; but by the “Pumping Lemma” it cannot be empty, either, so it must contain at least one letter. Now we are ready to “pump”. Since uvwxy is in L, uv 2wx 2 y must also be in L. Since v and x can’t both be empty,
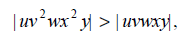
so we have added letters.
Both since vx does not contain all three distinct letters, we cannot have added the same number of each letter. Therefore, uv2wx2y cannot be in L.
Thus we have arrived at a “contradiction”. Hence our original assumption, that L is context free should be false. Hence the language L is not con text-free.
Example 1: Check whether the language given by
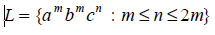
is a CFL or not.
Solution: Let s = anbnc2n, n being obtained from Pumping Lemma.
Then s = uvwxy, where 1 £| vx | £ n.
Therefore, vx cannot have all the three symbols a, b, c.
If you assume that vx has only a’s and b’s then we can shoose i such that uviwxiy has more than 2n occurrence of a or b and exactly 2n occurences of c.
Hence uv I wx i y∈L, which is a contradiction. Hence L is not a CFL.
Example 3 “If L is regular and L Í Σ* , then Σ* - L is also a regular set”—Prove this theorem.
Proof: Let L = T(M) where M = (Q, Σ,d, q , F ) 0 is a Finite Automata. We modify Σ,Q and d as follows:
(a) If a ∈Σ - Σ 1 , then the symbol ‘a’ will not appear in any string of T(M).
Therefore we can delete ‘a’ from S1 and all transitions defined by ‘a’.
Here T(M) is not affected.
(b) If Σ - Σ ¹Æ 1 , we can add a dead state d to Q. Let us define d(d, a) = d, for all ‘a’ in Σ and d(q, a) = d, for all q in Q and a in Σ - Σ1 .
Hence also T(M) is not affected.
Let us consider M obtained by applying (a) and (b) to S,Q and d. The new M is now written as (Q, Σ,d, q , F ) 0 . Let us define a new automaton ‘M’ such that M¢ = (Q, S,d,Q, F ), where M' differs fromM only in its final states. There w∈T (M' ) iff d(q0 , w) Q F ∈ - and w∈T (M).
Therefore, S* - L = T (M¢ ) is regular