Kirchoff's Voltage Law (Kvl)

Kirchoff’s Laws: Arguably the most common and useful set of laws for solving electric circuits are the Kirchoff’s voltage and current laws. Several other useful relationships can be derived based on these laws.

Kirchoff’s Voltage Law (KVL):  "The sum of all the voltages (rises and drops) around a closed loop is equal to zero.” In other words, the algebraic sum of all voltage rises is equal to the algebraic sum of all the voltage drops around a closed loop.

Example In each of the circuit diagrams in given figure, write the mesh equations using KVL.

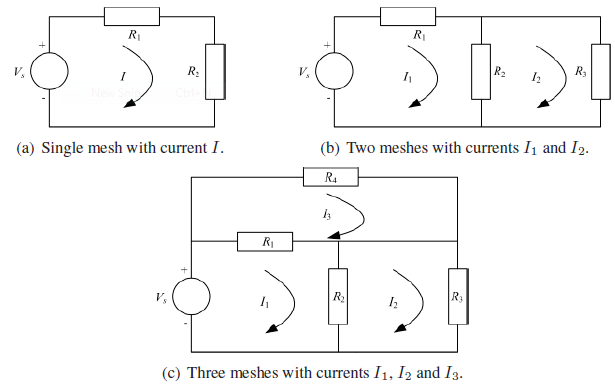
Figure(a) contains a single loop hence a single current, I is flowing around it. Therefore a single equation will result as given below
Vs = IR1 IR2

If Vs, R1 and R2 are known, then I can be found. Figure(b) contains two meshes with currents I1 and I2 hence there will be two equations as shown
below. Note that the branch containing R2 is common to both meshes with currents I1 and I2 flowing in opposite directions.

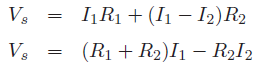Left loop
 

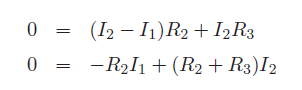Right loop

Given Vs,R1,R2 & R3, Equations can be solved simultaneously to evaluate I1 and I2. For the circuit diagram of Figure (c), three equations need to be written as follows. Also note that there is no circuit element shared between loops 2 and 3 hence I2 and I3 are independent of each other.

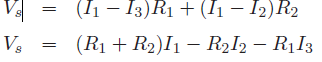Left bottom loop

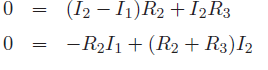
Right bottom loop

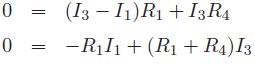Upper loop

If  Vs and resistors’ values are known, the mesh currents can be evaluated by solving upper three Equations simultaneously.