Rms Value Of An Ac Waveform
RMS Value of an AC Waveform: The average value of an AC waveform is NOT the same value as that for a DC waveforms average value. This is because the AC waveform is constantly changing with time and the heating effect given by the formula ( P = I 2.R ), will also be changing producing a positive power consumption. The equivalent average value for an alternating current system that provides the same power to the load as a DC equivalent circuit is called the "effective value".
This effective power in an alternating current system is therefore equal to: ( I 2.R.Average ). As power is proportional to current squared, the effective current, I will be equal to √ I 2 Ave. Therefore, the effective current in an AC system is called the Root Mean Squared or R.M.S. value and RMS values are the DC equivalent values that provide the same power to the load.
The effective or RMS value of an alternating current is measured in terms of the direct current value that produces the same heating effect in the same value resistance. The RMS value for any AC waveform can be found from the following modified average value formula.
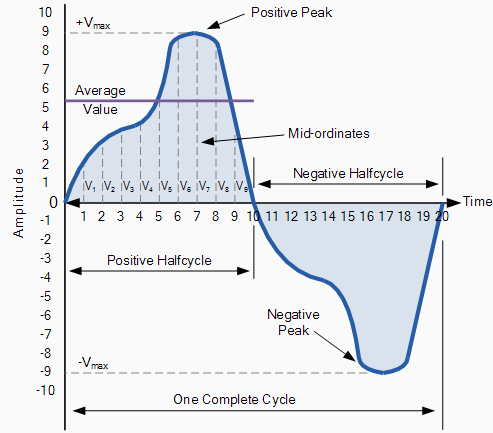
![]()
Where: n equals the number of mid-ordinates.
For a pure sinusoidal waveform this effective or R.M.S. value will always be equal to 1/√2 x Vmax which is equal to 0.707 x Vmax and this relationship holds true for RMS values of current. The RMS value for a sinusoidal waveform is always greater than the average value except for a rectangular waveform. In this case the heating effect remains constant so the average and the RMS values will be the same.
One final comment about R.M.S. values. Most multimeters, either digital or analogue unless otherwise stated only measure the R.M.S. values of voltage and current and not the average. Therefore when using a multimeter on a direct current system the reading will be equal to I = V/R and for an alternating current system the reading will be equal to Irms = Vrms/R.
Also, except for average power calculations, when calculating RMS or peak voltages, only use VRMS to find IRMS values, or peak voltage, Vp to find peak current, Ip values. Do not mix the two together average, RMS or peak values as they are completely different and your results will be incorrect.