Magnetic Circuit

Magnetic Circuit:  In this lesson, we shall acquaint the reader, primarily with the basic concepts of magnetic circuit and methods of solving it. Biot-Savart law for calculating magnetic field due to a known current distribution although fundamental and general in nature, requires an integration to be evaluated which sometimes become an uphill task. Fortunately, due to the specific nature of the problem, Ampere’s circuital law (much easier to apply) is adopted for calculating field in the core of a magnetic circuit. You will also understand the importance of B-H curve of a magnetic material and its use. The concept and analysis of linear and non linear magnetic circuit will be explained. The lesson will conclude with some worked out examples.

Key Words: mmf, flux, flux density, mean length, permeability, reluctance.

Before really starting, let us look at some magnetic circuits shown in the following figures.

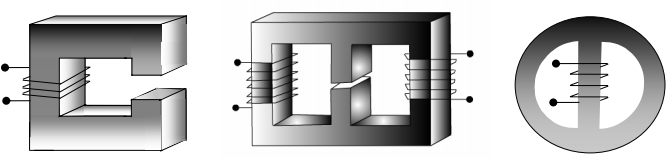fig....(A) (B)(C)

All of them have a magnetic material of regular geometric shape called  core. A coil having a number of turns (= N) of conducting material (say  copper) are wound over the core. This coil is called the exciting coil. When no current flows through the coil, we don’t expect any magnetic field or lines of forces to be present inside the core. However in presence of current in the coil, magnetic flux φ will be produced within the core. The strength of the flux, it will be shown, depends on the product of number of turns (N) of the coil and the current (i) it carries. The quantity  Ni called mmf (magnetomotive force) can  be thought as the cause in order to produce an effect in the form of flux φ within the core. Is it not somewhat similar to an electrical circuit problem where a voltage (emf) is applied (cause) and a current is produced (effect) in the circuit? Hence the term  magnetic circuit is used in relation to producing flux in the core by applying mmf (= Ni). We shall see more similarities between an electrical circuit and a magnetic circuit in due course as we go along further. At this point you may just note that a magnetic circuit may be as simple as shown in figure (A) with a single core and a single coil or as complex as having different core materials, air gap and multiple exciting coils as in figure (B).