Power Factor

Power Factor: The term cos φ in Equation P_av = 1/2 (V_mI_mcosφ)is called the power factor and is an important parameter in determining the amount of actual power dissipated in the load. In practise, power factor is used to specify the characteristics of a load.

For a purely resistive load φ = 0⁰, hence Unity Power Factor

For a capacitive type load I leads V , hence Leading power factor

For an inductive type load I lags V , hence Lagging power factor

From Equation P_rms = V_rmsI_rms cos φ, the current can be specified as

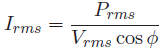
Clearly, for a fixed amount of demanded power, P, at a constant load voltage, V , a higher power factor draws less amount of current and hence low I²R losses in the transmission lines. A purely reactive load where φ → 90⁰ and cos φ → 0 will draw an excessively large amount of current and a power factor correction is required as discussed in the next section.

Real and Apparent Power It is important to highlight that in AC circuits, the product of voltage and current yields the apparent power which is measured in volt-amperes² or VA. The real AC power is given by Equation P_rms = V_rmsI_rms cos φ which is measured in Watts.

Example
An AC generator is rated at 900 kVA (450 V /2000 A). This is the apparent power and represents the highest current and voltage magnitudes the machine can output without temperature exceeding the recommended value. The load voltage, however, could be 230 V with a supplied current depending on the load impedance. The phase angle between the current and voltage determines the power factor and the real power can be calculated using

Equation P_rms = V_rmsI_rms cos φ.