Simple Parallel (Tank Circuit) Resonance
Simple parallel (tank circuit) resonance: A condition of resonance will be experienced in a tank circuit when the reactances of the capacitor and inductor are equal to each other. Because inductive reactance increases with increasing frequency and capacitive reactance decreases with increasing frequency, there will only be one frequency where these two reactances will be equal.
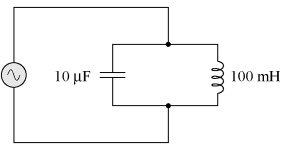
In the above circuit, we have a 10 μF capacitor and a 100 mH inductor. Since we know the equations for determining the reactance of each at a given frequency, and we're looking for that point where the two reactances are equal to each other, we can set the two reactance formulae equal to each other and solve for frequency algebraically:
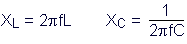
... setting the two equal to each other, representing a condition of equal reactance (resonance)...
![]()
Multiplying both sides by f eliminates the f term in the denominator of the fraction...
![]()
Dividing both sides by 2πL leaves f2 by itself on the left-hand side of the equation....
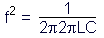
Taking the square root of both sides results in the final equation:
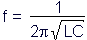
So there we have it: a formula to tell us the resonant frequency of a tank circuit, given the values of inductance (L) in Henrys and capacitance (C) in Farads. Plugging in the values of L and C in our example circuit, we arrive at a resonant frequency of 159.155 Hz.
What happens at resonance is quite interesting. With capacitive and inductive reactances equal to each other, the total impedance increases to infinity, meaning that the tank circuit draws no current from the AC power source! We can calculate the individual impedances of the 10 μF capacitor and the 100 mH inductor and work through the parallel impedance formula to demonstrate this mathematically:
XL = 2πfL
XL = 2*π*159.155 Hz*100 mH
XL = 100Ω
XC = 1/(2πfC)
XC = 1/(2*π*159.155 Hz*10 µF)
XC = 100Ω
As you might have guessed, I chose these component values to give resonance impedances that were easy to work with (100 Ω even). Now, we use the parallel impedance formula to see what happens to total Z:
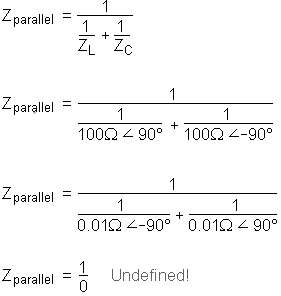
We can't divide any number by zero and arrive at a meaningful result, but we can say that the result approaches a value of infinity as the two parallel impedances get closer to each other. What this means in practical terms is that, the total impedance of a tank circuit is infinite (behaving as an open circuit) at resonance.