star-delta transformation/delta-star transformation: Three branches in an electrical network can be connected in numbers of forms but most common among them is either star or delta form. In delta connection three branches are so connected that they form a closed loop that is they are mesh connected. As these three branches are connected nose to tail they forms an triangular closed loop, this configuration is referred as delta connection. On the other hand when either terminal of three branches are connected to a common point to form a Y like pattern is known as star connection. But these star and delta connections can be transformed from one form to other. For simplifying complex network, it is often required delta to star or star to delta transformation.

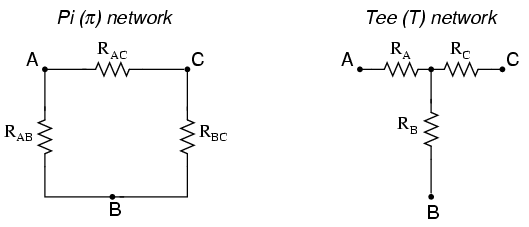
In many circuit applications, we encounter components connected together in one of two ways to form a three-terminal network: the “Delta,” or Δ (also known as the “Pi,” or π) configuration, and the “Y” (also known as the “T”) configuration.

                      

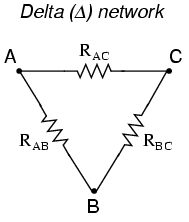
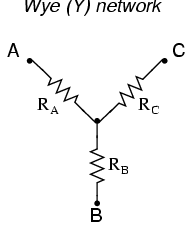
It is possible to calculate the proper values of resistors necessary to form one kind of network (Δ or Y) that behaves identically to the other kind, as analyzed from the terminal connections alone. That is, if we had two separate resistor networks, one Δ and one Y, each with its resistors hidden from view, with nothing but the three terminals (A, B, and C) exposed for testing, the resistors could be sized for the two networks so that there would be no way to electrically determine one network apart from the other. In other words, equivalent Δ and Y networks behave identically.

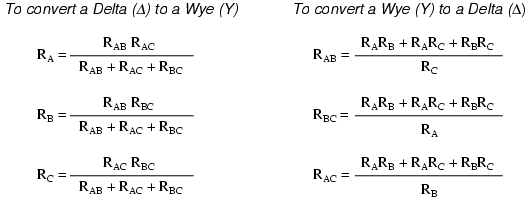
There are several equations used to convert one network to the other:

Δ and Y networks are seen frequently in 3-phase AC power systems (a topic covered in volume II of this book series), but even then they're usually balanced networks (all resistors equal in value) and conversion from one to the other need not involve such complex calculations. When would the average technician ever need to use these equations?

A prime application for Δ-Y conversion is in the solution of unbalanced bridge circuits, such as the one below:

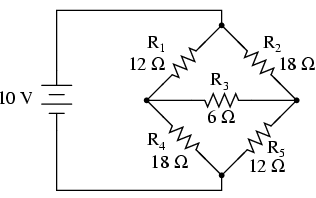
Solution of this circuit with Branch Current or Mesh Current analysis is fairly involved, and neither the Millman nor Superposition Theorems are of any help, since there's only one source of power. We could use Thevenin's or Norton's Theorem, treating R₃ as our load, but what fun would that be?

If we were to treat resistors R₁, R₂, and R₃ as being connected in a Δ configuration (R_ab, R_ac, and R_bc, respectively) and generate an equivalent Y network to replace them, we could turn this bridge circuit into a (simpler) series/parallel combination circuit: