Block Diagram Reduction

Block diagram reduction:

It is important to note that blocks can be connected in series only if the output of one block is not affected by the next following block. If there are any loading effects between the components, it is necessary to combine these components into a single block.

Any number of cascaded blocks representing non loading components can be replaced by a single block, the transfer function of which is simply the product of the individual transfer functions.

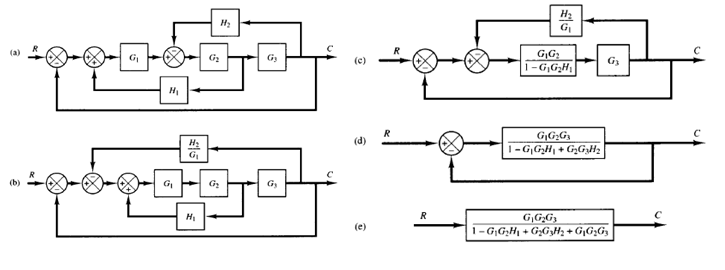
A complicated block diagram involving many feedback loops can be simplified by a step-by-step rearrangement, using rules of block diagram algebra. Some of these important rules are given in Table 1.

 They are obtained by writing the same equation in a different way. Simplification of the block diagram by rearrangements and substitutions considerably reduces the labor needed for subsequent mathematical analysis. It should be noted, however, that as the block diagram is simplified the transfer functions in new blocks become more complex because new poles and new zeros are generated.

In simplifying a block diagram, remember the following.

1. The product of the transfer functions in the feedforward direction must remain the same.

2. The product of the transfer functions around the loop must remain the same.

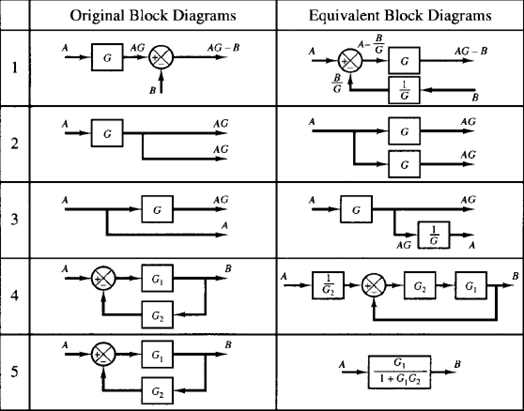
Table:1  Rules of Block Diagram Algebra

Example: