Comments On The Root-locus Plots
Comments on the root-locus plots:
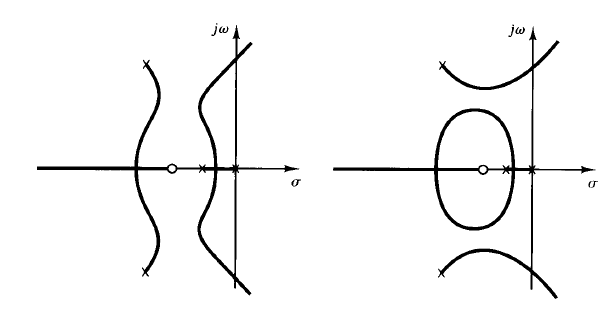
Fig: 1 Root-locus plot.
It is noted that the characteristic equation of the system whose open-loop transfer function is
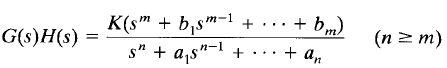
is an nth-degree algebraic equation in s.
If the order of the numerator of G(s)H(s) is lower than that of the denominator by two or more (which means that there are two or more zeros at infinity), then the coefficient a1 is the negative sum of the roots of the equation and is independent of K.
In such a case, if some of the roots move on the locus toward the left as K is increased, then the other roots must move toward the right as K is increased.
This information is helpful in finding the general shape of the root loci. It is also noted that a slight change in the pole-zero configuration may cause significant changes in the root-locus configurations.
Figure 1 demonstrates the fact that a slight change in the location of a zero or pole will make the root-locus configuration look quite different.