Nonminimum-phase Systems
Nonminimum-phase systems
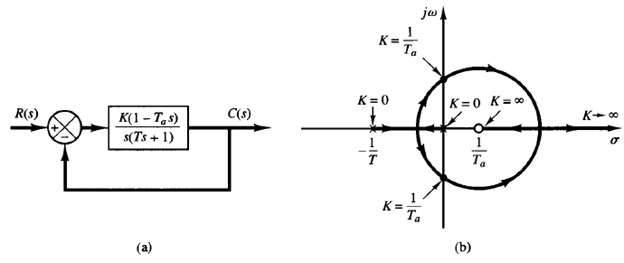
Fig: 1 (a) Nonminimum phase system; (b) root-locus plot.
If all the poles and zeros of a system lie in the left-half s plane, then the system is called minimum phase. If a system has at least one pole or zero in the right-half s plane, then the system is called nonminimum phase. The term nonminimum phase comes from the phase shift characteristics of such a system when subjected to sinusoidal inputs.
Consider the system shown in Figure 1(a). For this system
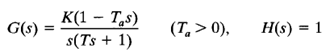
This is a nonminimum-phase system since there is one zero in the right-half s plane. For this system, the angle condition becomes
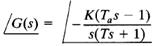
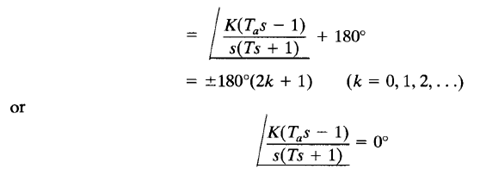
The root loci can be obtained from the above equation. Figure 1(b) shows a root-locus plot for this system. From the diagram, we see that the system is stable if the gain K is less than 1/Ta.