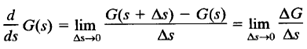Complex Variable & Complex Function
Complex variable:
A complex number has a real part and an imaginary part, both of which are constant. If the real part and/or imaginary part are variables, a complex number is called a complex variable. In the Laplace transformation we use the notation s as a complex variable; that is,
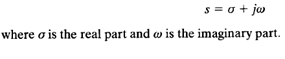
Complex function:
A complex function F(s), a function of s, has a real part and an imaginary part or
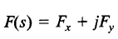
where Fx and Fy are real quantities. The magnitude of F(s) is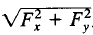
and the angle θ of F(s) is tan-1(Fy/Fx ). The angle is measured counterclockwise from the positive real axis. The complex conjugate of F(s) is F(s) = Fx - jFy.
Complex functions commonly encountered in linear control systems analysis are single-valued functions of s and are uniquely determined for a given value of s. A complex function G(s) is said to be analytic in a region if G(s) and all its derivatives exist in that region. The derivative of an analytic function G(s) is given by
