Minimum-phase Systems And Nonminimum-phase Systems
Minimum-phase systems and non-minimum-phase systems
Transfer functions having neither poles nor zeros in the right-half s plane are minimum-phase transfer functions, whereas those having poles and/or zeros in the right-half s plane are nonminimum-phase transfer functions. Systems with minimum-phase transfer functions are called minimum-phase systems, whereas those with nonminimum-phase transfer functions are called nonminimum-phase systems.
For systems with the same magnitude characteristic, the range in phase angle of the minimum-phase transfer function is minimum among all such systems, while the range in phase angle of any nonminimum-phase transfer function is greater than this minimum.
It is noted that for a minimum-phase system the transfer function can be uniquely determined from the magnitude curve alone. For a nonminimum-phase system, this is not the case. Multiplying any transfer function by all-pass filters does not alter the magnitude curve, but the phase curve is changed.
Consider as an example the two systems whose sinusoidal transfer functions are, respectively,
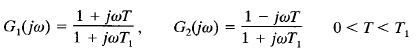
The pole-zero configurations of these systems are shown in Figure 1. The two sinusoidal transfer functions have the same magnitude characteristics, but they have different phase-angle characteristics, as shown in Figure 2. These two systems differ from each other by the factor
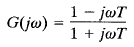
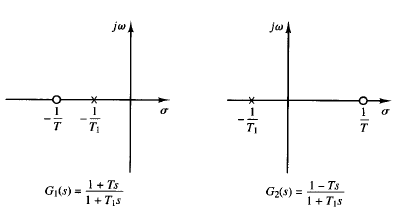
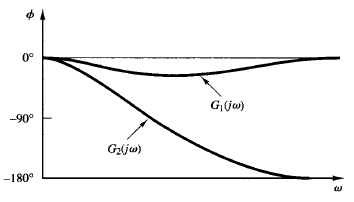
Fig: 1 Pole-zero configurations of a minimum phase system Fig: 2 Phase-angle characteristics of the systems
The magnitude of the factor (1 - jωt)/(1 jωt) is always unity. But the phase angle equals -2 tan-1 ωT and varies from 0° to -180° as ω is increased from zero to infinity.
As stated earlier, for a minimum-phase system, the magnitude and phase-angle characteristics are uniquely related. This means that if the magnitude curve of a system is specified over the entire frequency range from zero to infinity, then the phaseangle curve is uniquely determined, and vice versa. This, however, does not hold for a nonminimum-phase system.
Nonminimum-phase situations may arise in two different ways. One is simply when a system includes a nonminimum-phase element or elements. The other situation may arise in the case where a minor loop is unstable.
For a minimum-phase system, the phase angle at ω = ∞ becomes -900 (q - p), where p and q are the degrees of the numerator and denominator polynomials of the transfer function, respectively. For a nonminimum-phase system, the phase angle at ω = ∞ differs from -900 (q - p). In either system, the slope of the log-magnitude curve at ω = ∞ is equal to -20(q - p) dB/decade. It is therefore possible to detect whether the system is minimum phase by examining both the slope of the high-frequency asymptote of the log-magnitude curve and the phase angle at ω = ∞. If the slope of the log-magnitude curve as ω approaches infinity is -20(q - p) dB/decade and the phase angle at ω = ∞ is equal to -900 (q - p), then the system is minimum phase. Nonminimum-phase systems are slow in response because of their faulty behavior at the start of response. In most practical control systems, excessive phase lag should be carefully avoided. In designing a system, if fast speed of response is of primary importance, we should not use nonminimum-phase components. (A common example of nonminimum-phase elements that may be present in control system is transport lag.)
It is noted that the techniques of frequency-response analysis and design to be presented in this and the next chapter are valid for both minimum-phase and nonminimum phase systems.