Multiple-loop System Of A Polar Plot
Multiple-loop system of a polar plot
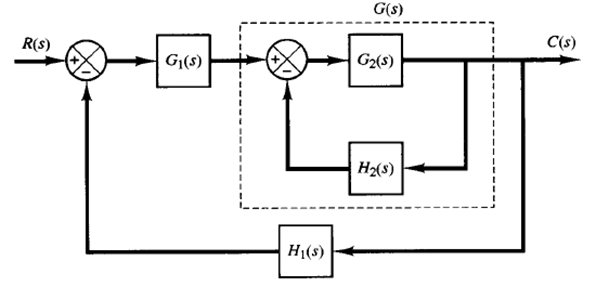
Fig: 1 Multiple-loop system
Consider the system shown in Figure 1. This is a multiple-loop system. The inner loop has the transfer function
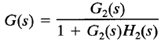
If G(s) is unstable, the effects of instability are to produce a pole or poles in the right half s plane. Then the characteristic equation of the inner loop, 1 G2(s)H2(s) = 0, has a zero or zeros in this portion of the plane. If G2(S) and H2(S) have P1 poles here, then the number Z1 of right-half plane zeros of 1 G2(s)H2(S) can be found from Z1 = N1 P1, where N1 is the number of clockwise encirclements of the -1 j0 point by the G2(s)H2(S) locus.
Since the open-loop transfer function of the entire system is given by G1(s)G(s)H1(s), the stability of this closed-loop system can be found from the Nyquist plot of G1l(s)G(s)H1(s) and knowledge of the right-half plane poles of G1(s)G(s)H1(s).
Notice that if a feedback loop is eliminated by means of block diagram reductions there is a possibility that unstable poles are introduced; if the feedforward branch is eliminated by means of block diagram reductions, there is a possibility that right-half plane zeros are introduced. Therefore, we must note all right-half plane poles and zeros as they appear from subsidiary loop reductions. This knowledge is necessary in determining the stability of multiple-loop systems.