Transfer Function Of A First Order Factor In Bode Diagram

Transfer function of a first order factor in Bode diagram

The transfer function 1/(1 jωT) has the characteristics of a low-pass filter. For frequencies above ω = 1/T, the log magnitude falls off rapidly toward -∞. This is essentially due to the presence of the time constant. In the low-pass filter, the output can follow a sinusoidal input faithfully at low frequencies. But as the input frequency is increased, the output cannot follow the input because a certain amount of time is required for the system to build up in magnitude. Thus, at high frequencies, the amplitude of the output approaches zero and the phase angle of the output approaches -90°. Therefore, if the input function contains many harmonics, then the low-frequency components are reproduced faithfully at the output, while the high-frequency components are attenuated in amplitude and shifted in phase. Thus, a first-order element yields exact, or almost exact, duplication only for constant or slowly varying phenomena.

An advantage of the Bode diagram is that for reciprocal factors, for example, the factor 1 jωT, the log-magnitude and the phase-angle curves need only be changed in sign. Since

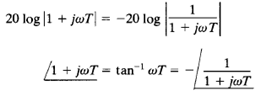
the corner frequency is the same for both cases. The slope of the high-frequency asymptote of 1 jω T is 20 dB/decade, and the phase angle varies from 0° to 90° as the frequency ω is increased from zero to infinity. The log-magnitude curve together with the asymptotes and the phase-angle curve for the factor 1 jωT are shown in Figure.

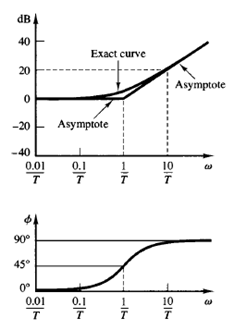
Fig: Log-magnitude curve together with the asymptotes and phase-angle curve

The shapes of phase-angle curves are the same for any factor of the form (1 jωT)^âˆ“¹. Hence, it is convenient to have a template for the phase-angle curve on cardboard. Then such a template may be used repeatedly for constructing phase-angle curves for any function of the form (1 jωT)^âˆ“¹. If such a template is not available, we have to locate several points on the curve. The phase angles of (1 jωT)^âˆ“¹ are

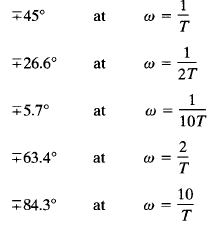
For the case where a given transfer function involves terms like (1 jωT)^âˆ“¹, a similar asymptotic construction may be made. The corner frequency is still at w =1/T, and the asymptotes are straight lines.

The low-frequency asymptote is a horizontal straight line at 0 dB, while the high-frequency asymptote has the slope of -20n dB/decade or 20n dB/decade. The error involved in the asymptotic expressions is n times that for (1 jωT)^âˆ“¹. The phase angle is n times that of (1 jωT)^âˆ“¹ at each frequency point.