Sensitivity And The Root Locus
Sensitivity and the root locus
One of the prime reasons for the use of negative feedback in control systems is the reduction of the effect of parameter variations. The effect of parameter variations can be described by a measure of the sensitivity of the system performance to specific parameter changes. The logarithmic sensitivity originally suggested by Bode is given as:
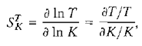
where the system transfer function is T(s) and the parameter of interest is K. In recent years, there has been an increased use of the pole-zero (j-plane) approach. Therefore, it has become useful to define a sensitivity measure in terms of the positions of the roots of the characteristic equation [7-9]. Because these roots represent the dominant modes of transient response, the effect of parameter variations on the position of the roots is an important and useful measure of the sensitivity. The root sensitivity of a system T(s) can be defined as

and K is a parameter affecting the roots. The root sensitivity relates the changes in the location of the root in the s-plane to the change in the parameter. The root sensitivity is related to the logarithmic sensitivity by the relation
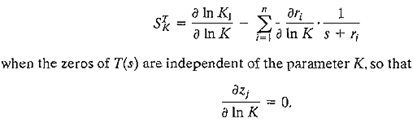
This logarithmic sensitivity can be readily obtained by determining the derivative of T(s), the equation of ith root of the system, with respect to K. For this particular case, when the gain of the system is independent of the parameter K, we have
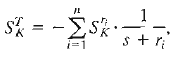
and the two sensitivity measures are directly related.
The evaluation of the root sensitivity for a control system can be readily accomplished by utilizing the root locus methods of the preceding section. The root sensitivity Sr1K may be evaluated at root –ri, by examining the root contours for the parameter K. We can change K by a small finite amount Δ K and determine the modified root -(r1 Δri) at K ΔK. Then, using Equation of the root sensitivity of a system, we have
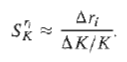
The equation above is an approximation that approaches the actual value of the sensitivity as ΔK → 0. An example will illustrate the process of evaluating the root sensitivity.