Denclue: Clustering Based On Density Distribution Functions
Introduction: DENCLUE (DENsity-based CLUstEring) is a clustering method based on a set of density distribution functions. The method is built on the following ideas: (1) the influence of each data point can be formally modeled using a mathematical function, called an influence function, which describes the impact of a data point within its neighborhood; (2) the overall density of the data space can be modeled analytically as the sum of the influence function applied to all data points; and (3) clusters can then be determined mathematically by identifying density attractors, where density attractors are local maxima of the overall density function.
Let x and y be objects or points in Fd, a d-dimensional input space. The influence function of data object y on x is a function, fyB : Fd ->R 0 , which is defined in terms of a basic influence function fB:
fyB (x) = fB(x, y)
This reflects the impact of y on x. In principle, the influence function can be an arbitrary function that can be determined by the distance between two objects in a neighborhood. The distance function, d(x, y), should be reflexive and symmetric, such as the Euclidean distance function (Section7.2.1).It can be used to compute a square wave influence function,
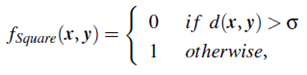
or a Gaussian influence function,
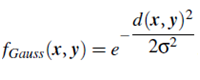
To help understand the concept of influence function, the following example offers some additional insight.