Skedbooks
←
Data Mining & Data Warehousing

Density-based Methods

Introduction: To discover clusters with arbitrary shape, density-based clustering methods have been developed. These typically regard clusters as dense regions of objects in the data space that are separated by regions of low density (representing noise). DBSCAN grows clusters according to a density-based connectivity analysis. OPTICS extends DBSCAN to produce a cluster ordering obtained from a wide range of parameter settings. DENCLUE clusters objects based on a set of density distribution functions.

1. DBSCAN: A Density-Based Clustering Method Based on Connected Regions with Sufficiently High Density

DBSCAN (Density-Based Spatial Clustering of Applications with Noise) is a density based clustering algorithm. The algorithm grows regions with sufficiently high density into clusters and discovers clusters of arbitrary shape in spatial databases with noise. It defines a cluster as a maximal set of density-connected points. The basic ideas of density-based clustering involve a number of new definitions. We intuitively present these definitions, and then follow up with an example.

  • The neighborhood within a radius e of a given object is called the e-neighborhood of the object.
  • If the e-neighborhood of an object contains at least a minimum number, Min Pts, of objects, then the object is called a core object.
  • Given a set of objects, D, we say that an object p is directly density-reachable from object q if p is within the e-neighborhood of q, and q is a core object.
  • An object p is density-reachable from object q with respect to e and Min Pts in a set of objects, D, if there is a chain of objects p1, … , pn, where p1 = q and pn = p such that pi 1 is directly density-reachable from pi with respect to e and Min Pts, for 1 ≤ i ≤ n, pi ∈D.
  • An object p is density-connected to object q with respect to e and Min Pts in a set of objects, D, if there is an object o 2 D such that both p and q are density-reachable from o with respect to e and Min Pts.

Density reach ability is the transitive closure of direct density reach ability, and this relationship is asymmetric. Only core objects are mutually density reachable. Density connectivity, however, is a symmetric relation.

2. OPTICS: Ordering Points to Identify the Clustering Structure: Although DBSCAN can cluster objects given input parameters such as e and Min Pts, it still leaves the user with the responsibility of selecting parameter values that will lead to the discovery of acceptable clusters. Actually, this is a problem associated with many other clustering algorithms. Such parameter settings are usually empirically set and difficult to determine, especially for real-world, high-dimensional data sets. Most algorithms are very sensitive to such parameter values: slightly different settings may lead to very different clustering’s of the data. Moreover, high-dimensional real data sets often have very skewed distributions, such that their intrinsic clustering structure may not be characterized by global density parameters.

To help overcome this difficulty, a cluster analysis method called OPTICS was proposed. Rather than produce a data set clustering explicitly, OPTICS computes an augmented cluster ordering for automatic and interactive cluster analysis. This ordering represents the density-based clustering structure of the data. It contains information that is equivalent to density-based clustering obtained from a wide range of parameter settings. The cluster ordering can be used to extract basic clustering information (such as cluster centers or arbitrary-shaped clusters) as well as provide the intrinsic clustering structure.

By examining DBSCAN, we can easily see that for a constant Min Pts value, density based clusters with respect to a higher density (i.e., a lower value for e) are completely contained in density-connected sets obtained with respect to a lower density. Recall that the parameter e is a distance—it is the neighborhood radius. Therefore, in order to produce a set or ordering of density-based clusters, we can extend the DBSCAN algorithm to process a set of distance parameter values at the same time. To construct the different clustering’s simultaneously, the objects should be processed in a specific order. This order selects an object that is density-reachable with respect to the lowest e value so that clusters with higher density (lower e) will be finished first.

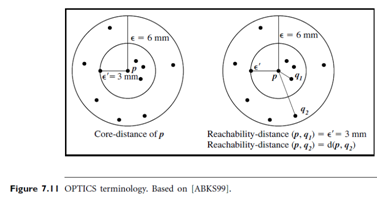
Based on this idea, two values need to be stored for each object—core-distance and reach ability-distance:

 

  • The core-distance of an object p is the smallest e0 value that makes {p} a core object. If p is not a core object, the core-distance of p is undefined.
  • The reach ability-distance of an object q with respect to another object p is the greater value of the core-distance of p and the Euclidean distance between p and q.