Pattern-growth Approach

Introduction: The Apriori-based approach has to use the breadth-first search (BFS) strategy because of its level-wise candidate generation. In order to determine whether a size-(k 1) graph is frequent; it must check all of its corresponding size-k sub-graphs to obtain an upper bound of its frequency. Thus, before mining any size-(k 1) sub-graph, the Apriori-like

Algorithm: Pattern Growth Graph. Simplistic pattern growth-based frequent substructure mining.

Input:

• g, a frequent graph;
• D, a graph data set;
• Min_sup, minimum support threshold.

Output:

• The frequent graph set, S.

Method:

S <- φ;

Call Pattern Growth Graph (g, D, min_sup, S);

procedure Pattern Growth Graph (g, D, min_sup, S)

1. if g ∈ S then return;

2. else insert g into S;

3. scan D once, find all the edges e such that g can be extended to g x e;

4. for each frequent g x e do

5.  Pattern Growth Graph(g x e, D, min sup, S);

6.  return;

approach usually has to complete the mining of size-k sub-graphs. Therefore, BFS is necessary in the Apriori-like approach. In contrast, the pattern-growth approach is more flexible regarding its search method. It can use breadth-first search as well as depth-first search (DFS), the latter of which consumes less memory.

A graph g can be extended by adding a new edge e. The newly formed graph is denoted by gx e. Edge e may or may not introduce a new vertex to g. If e introduces a new vertex, we denote the new graph by g x f e, otherwise, g xb e, where f or b indicates that the extension is in a forward or backward direction.

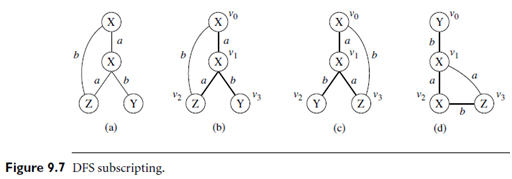Figure 9.6 illustrates a general framework for pattern growth–based frequent substructure mining. We refer to the algorithm as Pattern Growth Graph. For each discovered graph g, it performs extensions recursively until all the frequent graphs with g embedded are discovered. The recursion stops once no frequent graph can be generated. Pattern Growth Graph is simple, but not efficient. The bottleneck is at the inefficiency of extending a graph. The same graph can be discovered many times. For example, there may exist n different (n-1)-edge graphs that can be extended to the same n-edge graph. The repeated discovery of the same graph is computationally inefficient. We call a graph that is discovered a second time a duplicate graph. Although line 1 of Pattern Growth Graph gets rid of duplicate graphs, the generation and detection of duplicate graphs may increase the workload. In order to reduce the generation of duplicate graphs, each frequent graph should be extended as conservatively as possible. This principle leads to the design of several new algorithms. A typical such example is the gSpan algorithm, as described below. The gSpan algorithm is designed to reduce the generation of duplicate graphs. It need not search previously discovered frequent graphs for duplicate detection. It does not extend any duplicate graph, yet still guarantees the discovery of the complete set of frequent graphs.