A Bitonic Sorting Network

A bitonic sorting network

The first step in our construction of an efficient sorting network is to construct a comparison network that can sort any bitonic sequence: a sequence that monotonically increases and then monotonically decreases, or can be circularly shifted to become monotonically increasing and then monotonically decreasing. For example, the sequences 〈1, 4, 6, 8, 3, 2〉, 〈6, 9, 4, 2, 3, 5〉, and 〈9, 8, 3, 2, 4, 6〉 are all bitonic. As a boundary condition, we say that any sequence of just 1 or 2 numbers is bitonic. The zero-one sequences that are bitonic have a simple structure. They have the form 0ⁱ 1^j 0^k or the form 1ⁱ 0^j 1^k, for some i, j, k ≥ 0. Note that a sequence that is either monotonically increasing or monotonically decreasing is also bitonic.

The bitonic sorter that we shall construct is a comparison network that sorts bitonic sequences of 0's and 1's. Exercise 27.3-6 asks you to show that the bitonic sorter can sort bitonic sequences of arbitrary numbers.

The half-cleaner

A bitonic sorter is composed of several stages, each of which is called a half-cleaner. Each half-cleaner is a comparison network of depth 1 in which input line i is compared with line i n/2 for i = 1, 2,..., n/2. (We assume that n is even.) Figure 27.7 shows HALF-CLEANER[8], the half-cleaner with 8 inputs and 8 outputs.

Figure 27.7: The comparison network HALF-CLEANER[8]. Two different sample zero-one input and output values are shown. The input is assumed to be bitonic. A half-cleaner ensures that every output element of the top half is at least as small as every output element of the bottom half. Moreover, both halves are bitonic, and at least one half is clean.

When a bitonic sequence of 0's and 1's is applied as input to a half-cleaner, the half-cleaner produces an output sequence in which smaller values are in the top half, larger values are in the bottom half, and both halves are bitonic. In fact, at least one of the halves is clean-consisting of either all 0's or all 1's-and it is from this property that we derive the name "half-cleaner." (Note that all clean sequences are bitonic.) The next lemma proves these properties of half-cleaners.

The bitonic sorter

By recursively combining half-cleaners, as shown in Figure 27.9, we can build a bitonic sorter, which is a network that sorts bitonic sequences. The first stage of BITONIC-SORTER[n] consists of HALF-CLEANER[n]. Thus, we can complete the sort by using two copies of BITONIC-SORTER[n/2] to sort the two halves recursively. In Figure 27.9(a), the recursion has been shown explicitly, and in Figure 27.9(b), the recursion has been unrolled to show the progressively smaller half-cleaners that make up the remainder of the bitonic sorter. The depth D(n) of BITONIC-SORTER[n] is given by the recurrence

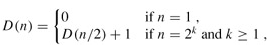
whose solution is D(n) = lg n.

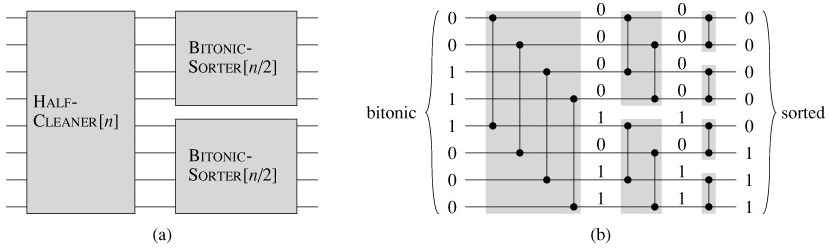
Figure 27.9: The comparison network BITONIC-SORTER[n], shown here for n = 8. (a) The recursive construction: HALF-CLEANER[n] followed by two copies of BITONIC-SORTER[n/2] that operate in parallel. (b) The network after unrolling the recursion. Each half-cleaner is shaded. Sample zero-one values are shown on the wires.

Thus, a zero-one bitonic sequence can be sorted by BITONIC-SORTER, which has a depth of lg n. It follows by the analog of the zero-one principle given as Exercise 27.3-6 that any bitonic sequence of arbitrary numbers can be sorted by this network.