A Merging Network

A merging network: Our sorting network will be constructed from merging networks, which are networks that can merge two sorted input sequences into one sorted output sequence. We modify BITONIC-SORTER[n] to create the merging network MERGER[n]. As with the bitonic sorter, we shall prove the correctness of the merging network only for inputs that are zero-one sequences.

The merging network is based on the following intuition. Given two sorted sequences, if we reverse the order of the second sequence and then concatenate the two sequences, the resulting sequence is bitonic. For example, given the sorted zero-one sequences X = 00000111 and Y = 00001111, we reverse Y to get Y^R= 11110000. Concatenating X and Y^R yields 0000011111110000, which is bitonic. Thus, to merge the two input sequences X and Y, it suffices to perform a bitonic sort on X concatenated with Y^R.

We can construct MERGER[n] by modifying the first half-cleaner of BITONIC- SORTER[n]. The key is to perform the reversal of the second half of the inputs implicitly. Given two sorted sequences 〈a₁, a₂,...,a_n/2〉 and 〈a_{n/2 1}, a_{n/2 2},..., a_n〉 to be merged, we want the effect of bitonically sorting the sequence 〈a₁, a₂,..., a_n/2, a_n, a_n-1,..., a_{n/2 1}〉. Since the first half-cleaner of BITONIC-SORTER[n] compares inputs i and n/2 i, for i = 1, 2,..., n/2, we make the first stage of the merging network compare inputs i and n - i 1. Figure 27.10 shows the correspondence. The only subtlety is that the order of the outputs from the bottom of the first stage of MERGER[n] are reversed compared with the order of outputs from an ordinary half-cleaner. Since the reversal of a bitonic sequence is bitonic.

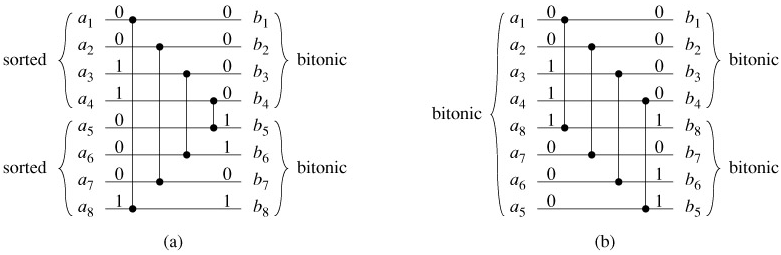
Figure 27.10: Comparing the first stage of MERGER[n] with HALF-CLEANER[n], for n = 8. (a) The first stage of MERGER[n] transforms the two monotonic input sequences 〈a₁, a₂,...,a_n/2〉 and 〈a_{n/2 1}, a_{n/2 2},...,a_n〉 into two bitonic sequences 〈b₁, b₂,...,b_n/2〉 and 〈b_{n/2 1}, b_{n/2 2},...,b_n〉. (b) The equivalent operation for HALF-CLEANER[n]. The bitonic input sequence 〈a₁, a₂,...,a_n/2-1, a_n/2, a_n, a_n-1,...,a_{n/2 2}, a_{n/2 1}〉 is transformed into the two bitonic sequences 〈b₁, b₂,...,b_n/2〉 and 〈b_n, b_n-1,...,b_{n/2 1}〉.

The resulting merging network is shown in Figure 27.11. Only the first stage of MERGER[n] is different from BITONIC-SORTER[n]. Consequently, the depth of MERGER[n] is lg n, the same as that of BITONIC-SORTER[n].

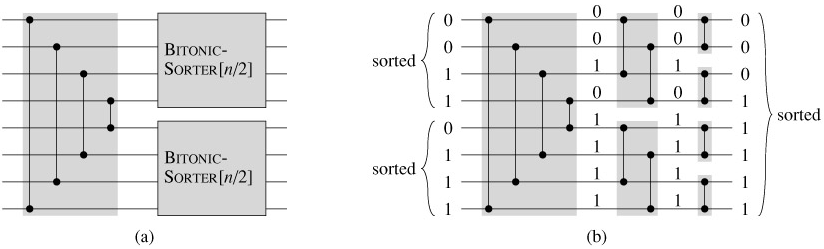
Figure 27.11: A network that merges two sorted input sequences into one sorted output sequence. The network MERGER[n] can be viewed as BITONIC-SORTER[n] with the first half-cleaner altered to compare inputs i and n - i 1 for i = 1, 2,..., n/2. Here, n = 8. (a) The network decomposed into the first stage followed by two parallel copies of BITONIC-SORTER[n/2]. (b) The same network with the recursion unrolled. Sample zero-one values are shown on the wires, and the stages are shaded.