Analysis Of Quicksort

Analysis of quicksort

In this section, we analyze the behavior of quicksort more rigorously. We begin with a worst-case analysis, which applies to either QUICKSORT or RANDOMIZED-QUICKSORT, and conclude with an average-case analysis of RANDOMIZED-QUICKSORT.

Worst-case analysis: We have seen that a worst-case split at every level of recursion in quicksort produces a Θ(n²) running time, which, intuitively, is the worst-case running time of the algorithm. We now prove this assertion.

Using the substitution method we can show that the running time of quicksort is O(n²). Let T (n) be the worst-case time for the procedure QUICKSORT on an input of size n. We have the recurrence

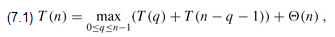
where the parameter q ranges from 0 to n - 1 because the procedure PARTITION produces two subproblems with total size n - 1. We guess that T (n) ≤ cn2 for some constant c. Substituting this guess into recurrence (7.1), we obtain

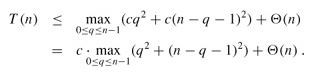
The expression q² (n-q-1)² achieves a maximum over the parameter's range 0 ≤ q ≤ n - 1 at either endpoint, as can be seen since the second derivative of the expression with respect to q is positive. This observation gives us the bound max_≤q≤n-1(q² (n - q - 1)²) ≤ (n - 1)² = n² - 2n 1. Continuing with our bounding of T (n), we obtain

since we can pick the constant c large enough so that the c(2n - 1) term dominates the Θ(n) term. Thus, T (n) = O(n²).

Expected running time

We have already given an intuitive argument why the average-case running time of RANDOMIZED-QUICKSORT is O(n lg n): if, in each level of recursion, the split induced by RANDOMIZED-PARTITION puts any constant fraction of the elements on one side of the partition, then the recursion tree has depth Θ(lg n), and O(n) work is performed at each level. Even if we add new levels with the most unbalanced split possible between these levels, the total time remains O(n lg n). We can analyze the expected running time of RANDOMIZED-QUICKSORT precisely by first understanding how the partitioning procedure operates and then using this understanding to derive an O(n lg n) bound on the expected running time. This upper bound on the expected running time, combined with the Θ(n lg n) best-case bound yields a Θ(n lg n) expected running time.

Running time and comparisons

The running time of QUICKSORT is dominated by the time spent in the PARTITION procedure. Each time the PARTITION procedure is called, a pivot element is selected, and this element is never included in any future recursive calls to QUICK-SORT and PARTITION. Thus, there can be at most n calls to PARTITION over the entire execution of the quicksort algorithm. One call to PARTITION takes O(1) time plus an amount of time that is proportional to the number of iterations of the for loop in lines 3-6. Each iteration of this for loop performs a comparison inline 4, comparing the pivot element to another element of the array A. Therefore, if we can count the total number of times that line 4 is executed, we can bound the total time spent in the for loop during the entire execution of QUICKSORT.

Lemma 7.1: mLet X be the number of comparisons performed in line 4 of PARTITION over the entire execution of QUICKSORT on an n-element array. Then the running time of QUICKSORT is O(n X).

Proof: By the discussion above, there are n calls to PARTITION, each of which does a constant amount of work and then executes the for loop some number of times. Each iteration of the for loop executes line 4.

Our goal, therefore is to compute X, the total number of comparisons performed in all calls to PARTITION. We will not attempt to analyze how many comparisons are made in each call to PARTITION. Rather, we will derive an overall bound on the total number of comparisons. To do so, we must understand when the algorithm compares two elements of the array and when it does not. For ease of analysis, we rename the elements of the array A as z₁, z₂,..., z_n, with z_i being the ith smallest element. We also define the set Z_ij = {z_i, z_{i 1},..., z_j} to be the set of elements between z_i and z_j, inclusive.

When does the algorithm compare z_i and z_j? To answer this question, we first observe that each pair of elements is compared at most once. Why? Elements are compared only to the pivot element and, after a particular call of PARTITION finishes, the pivot element used in that call is never again compared to any other elements.

Our analysis uses indicator random variables. We define

X_ij= I {z_i is compared to z_j} ,