Breadth-first Search

Breadth-first search: Breadth-first search is one of the simplest algorithms for searching a graph and the archetype for many important graph algorithms. Prim's minimum-spanning-tree algorithm and Dijkstra's single-source shortest-paths algorithm use ideas similar to those in breadth-first search.

Given a graph G = (V, E) and a distinguished source vertex s, breadth-first search systematically explores the edges of G to "discover" every vertex that is reachable from s. It computes the distance (smallest number of edges) from s to each reachable vertex. It also produces a "breadth-first tree" with root s that contains all reachable vertices. For any vertex v reachable from s, the path in the breadth-first tree from s to v corresponds to a "shortest path" from s to v in G, that is, a path containing the smallest number of edges. The algorithm works on both directed and undirected graphs.

Breadth-first search is so named because it expands the frontier between discovered and undiscovered vertices uniformly across the breadth of the frontier. That is, the algorithm discovers all vertices at distance k from s before discovering any vertices at distance k 1.

To keep track of progress, breadth-first search colors each vertex white, gray, or black. All vertices start out white and may later become gray and then black. A vertex is discovered the first time it is encountered during the search, at which time it becomes nonwhite. Gray and black vertices, therefore, have been discovered, but breadth-first search distinguishes between them to ensure that the search proceeds in a breadth-first manner. If (u, v) ∈ E and vertex u is black, then vertex v is either gray or black; that is, all vertices adjacent to black vertices have been discovered. Gray vertices may have some adjacent white vertices; they represent the frontier between discovered and undiscovered vertices.

Breadth-first search constructs a breadth-first tree, initially containing only its root, which is the source vertex s. Whenever a white vertex v is discovered in the course of scanning the adjacency list of an already discovered vertex u, the vertex v and the edge (u, v) are added to the tree. We say that u is the predecessor or parent of v in the breadth-first tree. Since a vertex is discovered at most once, it has at most one parent. Ancestor and descendant relationships in the breadth-first tree are defined relative to the root s as usual: if u is on a path in the tree from the root s to vertex v, then u is an ancestor of v and v is a descendant of u.

The breadth-first-search procedure BFS below assumes that the input graph G = (V, E) is represented using adjacency lists. It maintains several additional data structures with each vertex in the graph. The color of each vertex u ∈ V is stored in the variable color[u], and the predecessor of u is stored in the variable π[u]. If u has no predecessor (for example, if u = s or u has not been discovered), then π[u] = NIL. The distance from the source s to vertex u computed by the algorithm is stored in d[u]. The algorithm also uses a first-in, first-out queue Q to manage the set of gray vertices.

	BFS(G, s)
 1  for each vertex u ∈ V [G] - {s}
 2       do color[u] ← WHITE
 3          d[u] ← ∞
 4          π[u] ← NIL
 5  color[s] ← GRAY
 6  d[s] ← 0
 7  π[s] ← NIL
 8  Q ← Ø
 9  ENQUEUE(Q, s)
10  while Q ≠ Ø
11      do u ← DEQUEUE(Q)
12         for each v ∈ Adj[u]
13             do if color[v] = WHITE
14                   then color[v] ← GRAY
15                        d[v] ← d[u]   1
16                        π[v] ← u
17                        ENQUEUE(Q, v)
18         color[u] ← BLACK

Figure 22.3 illustrates the progress of BFS on a sample graph.

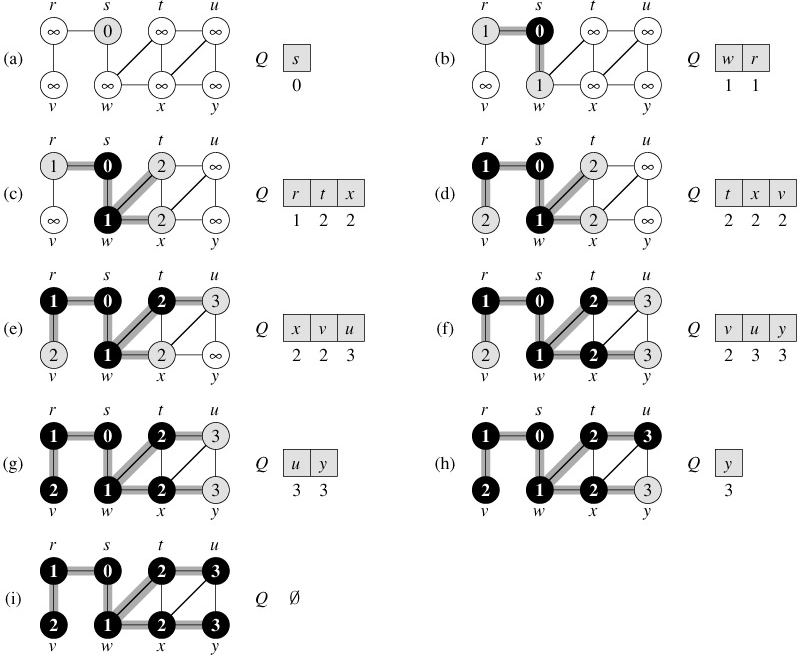
The procedure BFS works as follows. Lines 1-4 paint every vertex white, set d[u] to be infinity for each vertex u, and set the parent of every vertex to be NIL.Line 5 paints the source vertex s gray, since it is considered to be discovered when the procedure begins. Line 6 initializes d[s] to 0, and line 7 sets the predecessor of the source to be NIL. Lines 8-9 initialize Q to the queue containing just the vertex s.

The while loop of lines 10-18 iterates as long as there remain gray vertices, which are discovered vertices that have not yet had their adjacency lists fully examined. This while loop maintains the following invariant:

• At the test in line 10, the queue Q consists of the set of gray vertices.

Although we won't use this loop invariant to prove correctness, it is easy to see that it holds prior to the first iteration and that each iteration of the loop maintains the invariant. Prior to the first iteration, the only gray vertex, and the only vertex in Q, is the source vertex s. Line 11 determines the gray vertex u at the head of the queue Q and removes it from Q. The for loop of lines 12-17 considers each vertex v in the adjacency list of u. If v is white, then it has not yet been discovered, and the algorithm discovers it by executing lines 14-17. It is first grayed, and its distance d[v] is set to d[u] 1. Then, u is recorded as its parent. Finally, it is placed at the tail of the queue Q. When all the vertices on u's adjacency list have been examined, u is blackened in lines 11-18. The loop invariant is maintained because whenever a vertex is painted gray (in line 14) it is also enqueued (in line 17), and whenever a vertex is dequeued (in line 11) it is also painted black (in line 18).

The results of breadth-first search may depend upon the order in which the neighbors of a given vertex are visited in line 12: the breadth-first tree may vary, but the distances d computed by the algorithm will not.