Data Structures For Disjoint Sets

Disjoint-set operations: A disjoint-set data structure maintains a collection 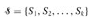of disjoint dynamic sets. Each set is identified by a representative, which is some member of the set. In some applications, it doesn't matter which member is used as the representative; we only care that if we ask for the representative of a dynamic set twice without modifying the set between the requests, we get the same answer both times. In other applications, there may be a prespecified rule for choosing the representative, such as choosing the smallest member in the set (assuming, of course, that the elements can be ordered).

As in the other dynamic-set implementations we have studied, each element of a set is represented by an object. Letting x denote an object, we wish to support the following operations:

• MAKE-SET(x) creates a new set whose only member (and thus representative) is x. Since the sets are disjoint, we require that x not already be in some other set.

• UNION(x, y) unites the dynamic sets that contain x and y, say S_x and S_y, into a new set that is the union of these two sets. The two sets are assumed to be disjoint prior to the operation. The representative of the resulting set is any member of S_x ∪ S_y, although many implementations of UNION specifically choose the representative of either S_x or S_y as the new representative. Since we require the sets in the collection to be disjoint, we "destroy" sets S_x and S_y, removing them from the collection .

• FIND-SET(x) returns a pointer to the representative of the (unique) set containing x.

Throughout this chapter, we shall analyze the running times of disjoint-set data structures in terms of two parameters: n, the number of MAKE-SET operations, and m, the total number of MAKE-SET, UNION, and FIND-SET operations. Since the sets are disjoint, each UNION operation reduces the number of sets by one. After n - 1 UNION operations, therefore, only one set remains. The number of UNION operations is thus at most n - 1. Note also that since the MAKE-SET operations are included in the total number of operations m, we have m ≥ n. We assume that the n MAKE-SET operations are the first n operations performed.

An application of disjoint-set data structures

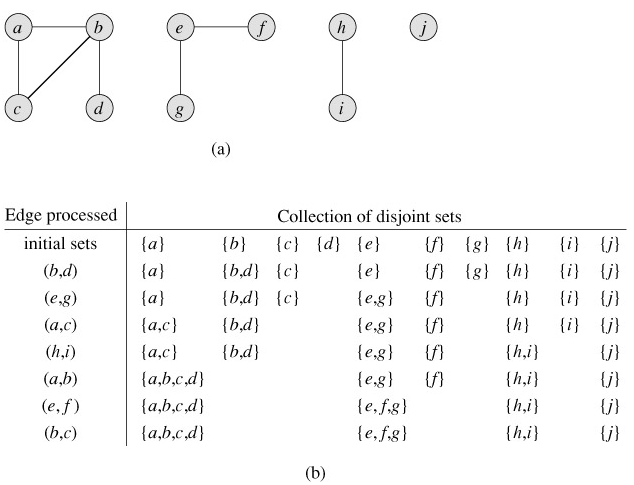
One of the many applications of disjoint-set data structures arises in determining the connected components of an undirected graph. Figure 21.1(a), for example, shows a graph with four connected components.

The procedure CONNECTED-COMPONENTS that follows uses the disjoint-set operations to compute the connected components of a graph. Once CONNECTED-COMPONENTS has been run as a preprocessing step, the procedure SAME-COMPONENT answers queries about whether two vertices are in the same connected component. (The set of vertices of a graph G is denoted by V [G], and the set of edges is denoted by E[G].)

	CONNECTED-COMPONENTS(G)
1  for each vertex v ∈ V[G]
2       do MAKE-SET(v)
3  for each edge (u, v) ∈ E[G]
4       do if FIND-SET(u) ≠ FIND-SET(v)
5             then UNION(u, v)

SAME-COMPONENT(u, v)
1  if FIND-SET(u) = FIND-SET(v)
2      then return TRUE
3      else return FALSE

The procedure CONNECTED-COMPONENTS initially places each vertex v in its own set. Then, for each edge (u, v), it unites the sets containing u and v. Thus, CONNECTED-COMPONENTS computes sets in such a way that the procedure SAME-COMPONENT can determine whether two vertices are in the same connected component. Figure 21.1(b) illustrates how the disjoint sets are computed by CONNECTED-COMPONENTS.

In an actual implementation of this connected-components algorithm, the representations of the graph and the disjoint-set data structure would need to reference each other. That is, an object representing a vertex would contain a pointer to the corresponding disjoint-set object, and vice-versa. These programming details depend on the implementation language, and we do not address them further here.