Line-segment Properties
Determining whether two line segments intersect: To determine whether two line segments intersect, we check whether each segment straddles the line containing the other. A segment  straddles a line if point p1 lies on one side of the line and point p2 lies on the other side. A boundary case arises if p1 or p2 lies directly on the line. Two line segments intersect if and only if either (or both) of the following conditions holds:
straddles a line if point p1 lies on one side of the line and point p2 lies on the other side. A boundary case arises if p1 or p2 lies directly on the line. Two line segments intersect if and only if either (or both) of the following conditions holds:
-
Each segment straddles the line containing the other.
-
An endpoint of one segment lies on the other segment. (This condition comes from the boundary case.)
The following procedures implement this idea. SEGMENTS-INTERSECT returns TRUE if segments  and
and  intersect and FALSE if they do not. It calls the subroutines DIRECTION, which computes relative orientations using the cross-product method above, and ON-SEGMENT, which determines whether a point known to be collinear with a segment lies on that segment.
intersect and FALSE if they do not. It calls the subroutines DIRECTION, which computes relative orientations using the cross-product method above, and ON-SEGMENT, which determines whether a point known to be collinear with a segment lies on that segment.
SEGMENTS-INTERSECT(p1, p2, p3, p4) 1 d1 ← DIRECTION(p3, p4, p1) 2 d2 ← DIRECTION(p3, p4, p2) 3 d3 ← DIRECTION(p1, p2, p3) 4 d4 ← DIRECTION(p1, p2, p4) 5 if ((d1 > 0 and d2 < 0) or (d1 < 0 and d2 > 0)) and ((d3 > 0 and d4 < 0) or (d3 < 0 and d4 > 0)) 6 then return TRUE 7 elseif d1 = 0 and ON-SEGMENT(p3, p4, p1) 8 then return TRUE 9 elseif d2 = 0 and ON-SEGMENT(p3, p4, p2) 10 then return TRUE 11 elseif d3 = 0 and ON-SEGMENT(p1, p2, p3) 12 then return TRUE 13 elseif d4 = 0 and ON-SEGMENT(p1, p2, p4) 14 then return TRUE 15 else return FALSE
DIRECTION(pi, pj, pk)
1 return (pk - pi) × (pj - pi)
ON-SEGMENT(pi, pj, pk) 1 if min(xi, xj) ≤ xk ≤ max(xi, xj) and min(yi, yj) ≤ yk ≤ max(yi, yj) 2 then return TRUE 3 else return FALSE
SEGMENTS-INTERSECT works as follows. Lines 1-4 compute the relative orientation di of each endpoint pi with respect to the other segment. If all the relative orientations are nonzero, then we can easily determine whether segments 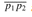 and
and  intersect, as follows. Segment
intersect, as follows. Segment 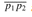 straddles the line containing segment
straddles the line containing segment  if directed segments
if directed segments 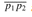 and
and  have opposite orientations relative to
have opposite orientations relative to  . In this case, the signs of d1 and d2 differ. Similarly,
. In this case, the signs of d1 and d2 differ. Similarly, 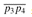 straddles the line containing
straddles the line containing 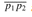 if the signs of d3 and d4 differ. If the test of line 5 is true, then the segments straddle each other, and SEGMENTS-INTERSECT returns TRUE. Figure 33.3(a) shows this case. Otherwise, the segments do not straddle each other's lines, although a boundary case may apply. If all the relative orientations are nonzero, no boundary case applies. All the tests against 0 in lines 7-13 then fail, and SEGMENTS-INTERSECT returns FALSE in line 15. Figure 33.3(b) shows this case.
if the signs of d3 and d4 differ. If the test of line 5 is true, then the segments straddle each other, and SEGMENTS-INTERSECT returns TRUE. Figure 33.3(a) shows this case. Otherwise, the segments do not straddle each other's lines, although a boundary case may apply. If all the relative orientations are nonzero, no boundary case applies. All the tests against 0 in lines 7-13 then fail, and SEGMENTS-INTERSECT returns FALSE in line 15. Figure 33.3(b) shows this case.

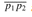 and
and 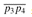 straddle each other's lines. Because
straddle each other's lines. Because 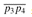 straddles the line containing
straddles the line containing 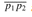 , the signs of the cross products (p3 - p1) × (p2 - p1) and (p4 - p1) × (p2 - p1) differ. Because
, the signs of the cross products (p3 - p1) × (p2 - p1) and (p4 - p1) × (p2 - p1) differ. Because 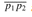 straddles the line containing
straddles the line containing 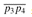 , the signs of the cross products (p1 - p3) × (p4 - p3) and (p2 - p3) × (p4 - p3) differ. (b) Segment
, the signs of the cross products (p1 - p3) × (p4 - p3) and (p2 - p3) × (p4 - p3) differ. (b) Segment 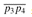 straddles the line containing
straddles the line containing 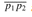 , but
, but 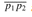 does not straddle the line containing
does not straddle the line containing 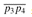 . The signs of the cross products (p1 - p3) × (p4 - p3) and (p2 - p3) × (p4 - p3) are the same. (c) Point p3 is collinear with
. The signs of the cross products (p1 - p3) × (p4 - p3) and (p2 - p3) × (p4 - p3) are the same. (c) Point p3 is collinear with 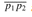 and is between p1 and p2. (d) Point p3 is collinear with
and is between p1 and p2. (d) Point p3 is collinear with 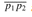 , but it is not between p1 and p2. The segments do not intersect.
, but it is not between p1 and p2. The segments do not intersect.
A boundary case occurs if any relative orientation dk is 0. Here, we know that pk is collinear with the other segment. It is directly on the other segment if and only if it is between the endpoints of the other segment. The procedure ON-SEGMENT returns whether pk is between the endpoints of segment  , which will be the other segment when called in lines 7-13; the procedure assumes that pk is collinear with segment
, which will be the other segment when called in lines 7-13; the procedure assumes that pk is collinear with segment  . Figures 33.3(c) and (d) show cases with collinear points. In Figure 33.3(c), p3 is on
. Figures 33.3(c) and (d) show cases with collinear points. In Figure 33.3(c), p3 is on 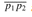 , and so SEGMENTS-INTERSECT returns TRUE in line 12. No endpoints are on other segments in Figure 33.3(d), and so SEGMENTS-INTERSECT returns FALSE in line 15.
, and so SEGMENTS-INTERSECT returns TRUE in line 12. No endpoints are on other segments in Figure 33.3(d), and so SEGMENTS-INTERSECT returns FALSE in line 15.