Operations On Binomial Heaps

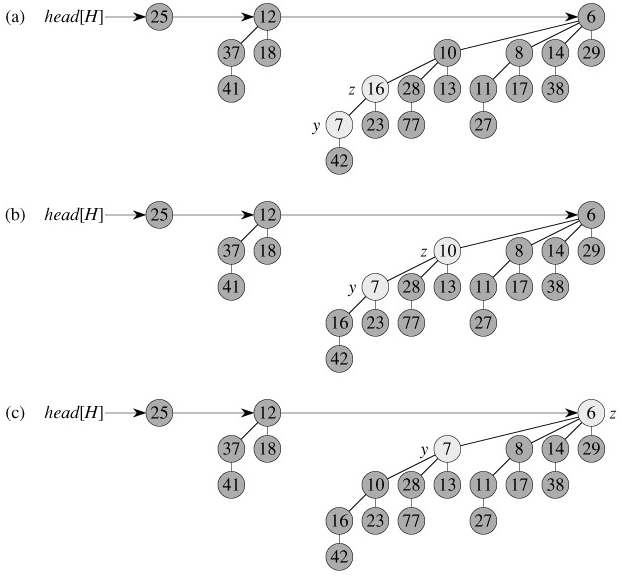
Figure 19.8: The action of BINOMIAL-HEAP-DECREASE-KEY. (a) The situation just before line 6 of the first iteration of the while loop. Node y has had its key decreased to 7, which is less than the key of y's parent z. (b) The keys of the two nodes are exchanged, and the situation just before line 6 of the second iteration is shown. Pointers y and z have moved up one level in the tree, but min-heap order is still violated. (c) After another exchange and moving pointers y and z up one more level, we find that min-heap order is satisfied, so the while loop terminates.

The BINOMIAL-HEAP-DECREASE-KEY procedure takes O(lg n) time. By property 2 of Lemma 19.1, the maximum depth of x is ⌊lg n⌋, so the while loop of lines 6-10 iterates at most ⌊lg n⌋ times.

Deleting a key

It is easy to delete a node x's key and satellite information from binomial heap H in O(lg n) time. The following implementation assumes that no node currently in the binomial heap has a key of -∞.

		BINOMIAL-HEAP-DELETE(H, x)
1  BINOMIAL-HEAP-DECREASE-KEY(H, x, -∞)
2  BINOMIAL-HEAP-EXTRACT-MIN(H)

The BINOMIAL-HEAP-DELETE procedure makes node x have the unique minimum key in the entire binomial heap by giving it a key of -∞. It then bubbles this key and the associated satellite information up to a root by calling BINOMIAL-HEAP-DECREASE-KEY. This root is then removed from H by a call of BINOMIAL-HEAP-EXTRACT-MIN.

The BINOMIAL-HEAP-DELETE procedure takes O(lg n) time.