Representing Rooted Trees

Representing rooted trees: The methods for representing lists given in the last sessions extend to any homogeneous data structure. In this section, we look specifically at the problem of representing rooted trees by linked data structures. We first look at binary trees, and then we present a method for rooted trees in which nodes can have an arbitrary number of children.

We represent each node of a tree by an object. As with linked lists, we assume that each node contains a key field. The remaining fields of interest are pointers to other nodes, and they vary according to the type of tree.

Binary trees

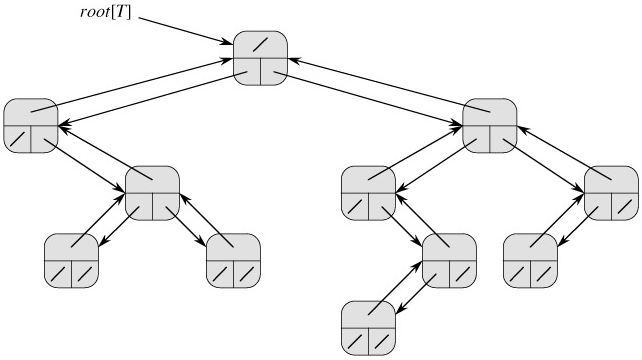
As shown in Figure 10.9, we use the fields p, left, and right to store pointers to the parent, left child, and right child of each node in a binary tree T . If p[x] = NIL, then x is the root. If node x has no left child, then left[x] = NIL, and similarly for the right child. The root of the entire tree T is pointed to by the attribute root[T]. If root[T] = NIL, then the tree is empty.

Figure 10.9: The representation of a binary tree T. Each node x has the fields p[x] (top), left[x] (lower left), and right[x] (lower right). The key fields are not shown.

Rooted trees with unbounded branching

The scheme for representing a binary tree can be extended to any class of trees in which the number of children of each node is at most some constant k: we replace the left and right fields by child₁, child₂,..., child_k. This scheme no longer works when the number of children of a node is unbounded, since we do not know how many fields (arrays in the multiple-array representation) to allocate in advance. Moreover, even if the number of children k is bounded by a large constant but most nodes have a small number of children, we may waste a lot of memory.

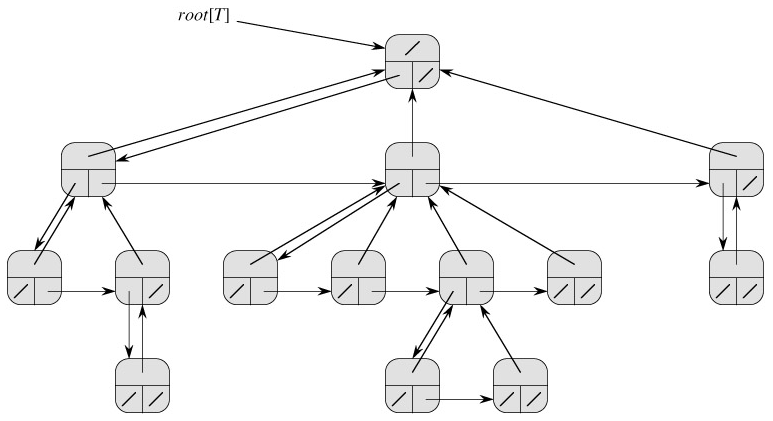
Fortunately, there is a clever scheme for using binary trees to represent trees with arbitrary numbers of children. It has the advantage of using only O(n) space for any n-node rooted tree. The left-child, right-sibling representation is shown in Figure 10.10. As before, each node contains a parent pointer p, and root[T] points to the root of tree T . Instead of having a pointer to each of its children, however, each node x has only two pointers:

Figure 10.10: The left-child, right-sibling representation of a tree T . Each node x has fields p[x] (top), left-child[x] (lower left), and right-sibling[x] (lower right). Keys are not shown.

left-child[x] points to the leftmost child of node x, and
right-sibling[x] points to the sibling of x immediately to the right.

If node x has no children, then left-child[x] = NIL, and if node x is the rightmost child of its parent, then right-sibling[x] = NIL.