String Matching With Finite Automata

In order to specify the string-matching automaton corresponding to a given pattern P[1 ‥ m], we first define an auxiliary function σ , called the suffix function corresponding to P. The function σ is a mapping from Σ* to {0, 1, . . . , m} such that σ(x) is the length of the longest prefix of P that is a suffix of x:

σ(x) = max {k : P_k ⊐ x}.

The suffix function σ is well defined since the empty string P₀ = ε is a suffix of every string. As examples, for the pattern P = ab, we have σ(ε) = 0, σ(ccaca) = 1, and σ(ccab) = 2. For a pattern P of length m, we have σ(x) = m if and only if P ⊐ x. It follows from the definition of the suffix function that if x ⊐ y, then σ(x) ≤ σ(y).

We define the string-matching automaton that corresponds to a given pattern P[1 ‥ m] as follows.

The state set Q is {0, 1, . . . , m}. The start state q₀ is state 0, and state m is the only accepting state.
The transition function δ is defined by the following equation, for any state q and character a:

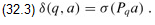
Here is an intuitive rationale for defining δ(q, a) = σ(P_qa). The machine maintains as an invariant of its operation that

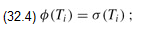
In words, this means that after scanning the first i characters of the text string T , the machine is in state φ(T_i) = q, where q = σ(T_i) is the length of the longest suffix of T_i that is also a prefix of the pattern P. If the next character scanned is T [i 1] = a, then the machine should make a transition to state σ(T_{i 1}) = σ(T_ia). The proof of the theorem shows that σ(T_ia) = σ(P_qa). That is, to compute the length of the longest suffix of T_ia that is a prefix of P, we can compute the longest suffix of P_qa that is a prefix of P. At each state, the machine only needs to know the length of the longest prefix of P that is a suffix of what has been read so far. Therefore, setting δ(q, a) = σ(P_qa) maintains the desired invariant (32.4). This informal argument will be made rigorous shortly.

In the string-matching automaton of Figure 32.7, for example, δ(5, b) = 4. We make this transition because if the automaton reads a b in state q = 5, then P_q b = ababab, and the longest prefix of P that is also a suffix of ababab is P₄ = abab.

To clarify the operation of a string-matching automaton, we now give a simple, efficient program for simulating the behavior of such an automaton (represented by its transition function δ) in finding occurrences of a pattern P of length m in an input text T [1 ‥ n]. As for any string-matching automaton for a pattern of length m, the state set Q is {0, 1, . . . , m}, the start state is 0, and the only accepting state is state m.

	FINITE-AUTOMATON-MATCHER(T, δ, m)
1  n ← length[T]
2  q ← 0
3  for i ← 1 to n
4      do q ← δ(q, T[i])
5         if q = m
6            then print "Pattern occurs with shift" i - m

The simple loop structure of FINITE-AUTOMATON-MATCHER implies that its matching time on a text string of length n is Θ(n). This matching time, however, does not include the preprocessing time required to compute the transition function δ. We address this problem later, after proving that the procedure FINITE-AUTOMATON-MATCHER operates correctly.

Consider the operation of the automaton on an input text T [1 ‥ n]. We shall prove that the automaton is in state σ(T_i) after scanning character T [i]. Since σ(T_i) = m if and only if P ⊐ T_i, the machine is in the accepting state m if and only if the pattern P has just been scanned. To prove this result, we make use of the following two lemmas about the suffix function σ.