The Floyd-warshall Algorithm
For k ≥ 1, if we take the path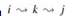 
, where k ≠ j, then the predecessor of j we choose is the same as the predecessor of j we chose on a shortest path from k with all intermediate vertices in the set {1, 2,...,k - 1}. Otherwise, we choose the same predecessor of j that we chose on a shortest path from i with all intermediate vertices in the set {1, 2,..., k - 1}. Formally, for k ≥ 1,
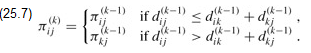
We leave the incorporation of the Π(k) matrix computations into the FLOYD-WARSHALL procedure. Figure 25.4 shows the sequence of Π(k) matrices that the resulting algorithm computes for the graph of Figure 25.1.The exercise also asks for the more difficult task of proving that the predecessor subgraph Gπ,i is a shortest-paths tree with root i.
Transitive closure of a directed graph: Given a directed graph G = (V, E) with vertex set V = {1, 2,...,n}, we may wish to find out whether there is a path in G from i to j for all vertex pairs i, j ∈ V. The transitive closure of G is defined as the graph G* = (V, E*), where E*= {(i, j) : there is a path from vertex i to vertex j in G}. One way to compute the transitive closure of a graph in Θ(n3) time is to assign a weight of 1 to each edge of E and run the Floyd-Warshall algorithm. If there is a path from vertex i to vertex j, we get dij < n. Otherwise, we get dij = ∞.
There is another, similar way to compute the transitive closure of G in Θ(n3) time that can save time and space in practice. This method involves substitution of the logical operations ∨ (logical OR) and ∧ (logical AND) for the arithmetic operations min and in the Floyd-Warshall algorithm. For i, j, k = 1, 2,...,n, we define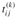 
to be 1 if there exists a path in graph G from vertex i to vertex j with all intermediate vertices in the set {1, 2,..., k}, and 0 otherwise. We construct the transitive closure G* = (V, E*) by putting edge (i, j) into E* if and only if 
. A recursive definition of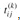 
, analogous to recurrence (25.5), is
and for k ≥ 1,
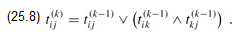
As in the Floyd-Warshall algorithm, we compute the matrices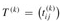 
in order of increasing k.
TRANSITIVE-CLOSURE(G) 1 n ← |V[G]| 2 for i ← 1 to n 3 do for j ← 1 to n 4 do if i = j or (i, j) ∈ E[G] 5 then
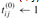
6 else
7 for k ← 1 to n 8 do for i ← 1 to n 9 do for j ← 1 to n 10 do
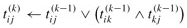
11 return T(n)
Figure 25.5 shows the matrices T(k) computed by the TRANSITIVE-CLOSURE procedure on a sample graph. The TRANSITIVE-CLOSURE procedure, like the Floyd-Warshall algorithm, runs in Θ(n3) time. On some computers, though, logical operations on single-bit values execute faster than arithmetic operations on integer words of data. Moreover, because the direct transitive-closure algorithm uses only boolean values rather than integer values, its space requirement is less than the Floyd-Warshall algorithm's by a factor corresponding to the size of a word of computer storage.
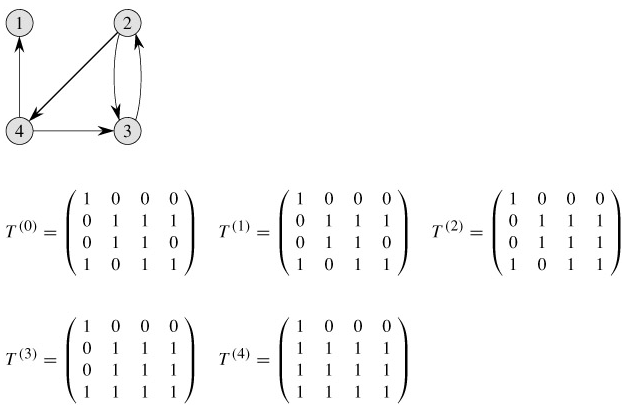Figure 25.5: A directed graph and the matrices T(k) computed by the transitive-closure algorithm.