The Ford-fulkerson Method
The Ford-Fulkerson method
This section presents the Ford-Fulkerson method for solving the maximum-flow problem. We call it a "method" rather than an "algorithm" because it encompasses several implementations with differing running times. The Ford-Fulkerson method depends on three important ideas that transcend the method and are relevant to many flow algorithms and problems: residual networks, augmenting paths, and cuts. These ideas are essential to the important max-flow min-cut theorem , which characterizes the value of a maximum flow in terms of cuts of the flow network. We end this section by presenting one specific implementation of the Ford-Fulkerson method and analyzing its running time.
The Ford-Fulkerson method is iterative. We start with f(u, v) = 0 for all u, v ∈ V, giving an initial flow of value 0. At each iteration, we increase the flow value by finding an "augmenting path," which we can think of simply as a path from the source s to the sink t along which we can send more flow, and then augmenting the flow along this path. We repeat this process until no augmenting path can be found. The max-flow min-cut theorem will show that upon termination, this process yields a maximum flow.
FORD-FULKERSON-METHOD(G, s, t) 1 initialize flow f to 0 2 while there exists an augmenting path p 3 do augment flow f along p 4 return f
Residual networks
Intuitively, given a flow network and a flow, the residual network consists of edges that can admit more flow. More formally, suppose that we have a flow network G = (V, E) with source s and sink t. Let f be a flow in G, and consider a pair of vertices u, v ∈ V. The amount of additional flow we can push from u to v before exceeding the capacity c(u, v) is the residual capacity of (u, v), given by
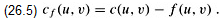
For example, if c(u, v) = 16 and f(u, v) = 11, then we can increase f(u, v) by cf (u, v) = 5 units before we exceed the capacity constraint on edge (u, v). When the flow f(u, v) is negative, the residual capacity cf (u, v) is greater than the capacity c(u, v). For example, if c(u, v) = 16 and f(u, v) = -4, then the residual capacity cf (u, v) is 20. We can interpret this situation as follows. There is a flow of 4 units from v to u, which we can cancel by pushing a flow of 4 units from u to v. We can then push another 16 units from u to v before violating the capacity constraint on edge (u, v). We have thus pushed an additional 20 units of flow, starting with a flow f(u, v) = -4, before reaching the capacity constraint.
Given a flow network G = (V, E) and a flow f, the residual network of G induced by f is Gf = (V, Ef), where
Ef = {(u, v) ∈ V × V : cf(u, v) > 0}.
That is, as promised above, each edge of the residual network, or residual edge, can admit a flow that is greater than 0. Figure 26.3(a) repeats the flow network G and flow f of Figure 26.1(b), and Figure 26.3(b) shows the corresponding residual network Gf.

The edges in Ef are either edges in E or their reversals. If f(u, v) < c(u, v) for an edge (u, v) ∈ E, then cf(u, v) = c(u, v) - f(u, v) > 0 and (u, v) ∈ Ef. If f(u, v) > 0 for an edge (u, v) ∈ E, then f (v, u) < 0. In this case, cf(v, u) = c(v, u) - f(v, u) > 0, and so (v, u) ∈ Ef. If neither (u, v) nor (v, u) appears in the original network, then c(u, v) = c(v, u) = 0, f(u, v)> = f(v, u) = 0, and cf(u, v) = cf(v, u) = 0. We conclude that an edge (u, v) can appear in a residual network only if at least one of (u, v) and (v, u) appears in the original network, and thus
|Ef| ≤ 2 |E|.
Observe that the residual network Gf is itself a flow network with capacities given by cf. The following lemma shows how a flow in a residual network relates to a flow in the original flow network.