The Naive String-matching Algorithm
The naive string-matching algorithm
The naive algorithm finds all valid shifts using a loop that checks the condition P[1 ‥ m] = T [s 1 ‥ s m] for each of the n - m 1 possible values of s.
NAIVE-STRING-MATCHER(T, P) 1 n ← length[T] 2 m ← length[P] 3 for s ← 0 to n - m 4 do if P[1 ‥ m] = T[s 1 ‥ s m] 5 then print "Pattern occurs with shift" s
The naive string-matching procedure can be interpreted graphically as sliding a "template" containing the pattern over the text, noting for which shifts all of the characters on the template equal the corresponding characters in the text, as illustrated in Figure 32.4. The for loop beginning on line 3 considers each possible shift explicitly. The test on line 4 determines whether the current shift is valid or not; this test involves an implicit loop to check corresponding character positions until all positions match successfully or a mismatch is found. Line 5 prints out each valid shift s.
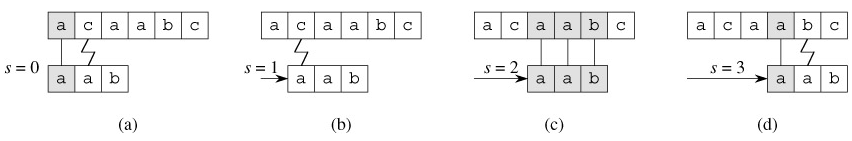
Procedure NAIVE-STRING-MATCHER takes time O((n - m 1)m), and this bound is tight in the worst case. For example, consider the text string an (a string of n a's) and the pattern am. For each of the n - m 1 possible values of the shift s, the implicit loop on line 4 to compare corresponding characters must execute m times to validate the shift. The worst-case running time is thus Θ((n - m 1)m), which is Θ(n2) if m = ⌊n/2⌋. The running time of NAIVE-STRING-MATCHER is equal to its matching time, since there is no preprocessing.
As we shall see, NAIVE-STRING-MATCHER is not an optimal procedure for this problem. Indeed, in this chapter we shall show an algorithm with a worst-case preprocessing time of Θ(m) and a worst-case matching time of Θ(n). The naive string-matcher is inefficient because information gained about the text for one value of s is entirely ignored in considering other values of s. Such information can be very valuable, however. For example, if P = aaab and we find that s = 0 is valid, then none of the shifts 1, 2, or 3 are valid, since T [4] = b. In the following sections, we examine several ways to make effective use of this sort of information.