Some Special Simple Graphs

Some Special Simple Graphs

EXAMPLE 1 Complete Graphs A complete graph on n vertices, denoted by Kn, is a simple graph that contains exactly one edge between each pair of distinct vertices. The graphs Kn, for n = 1, 2, 3, 4, 5, 6, are displayed in Figure 3. A simple graph for which there is at least one pair of distinct vertex not connected by an edge is called noncomplete.

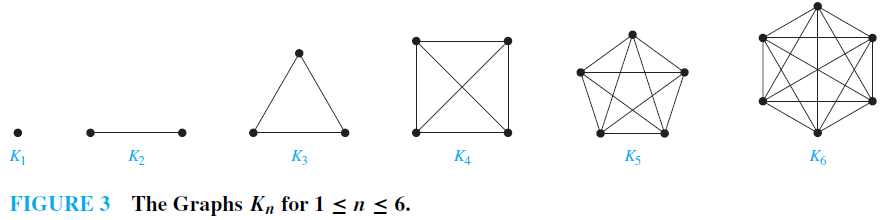
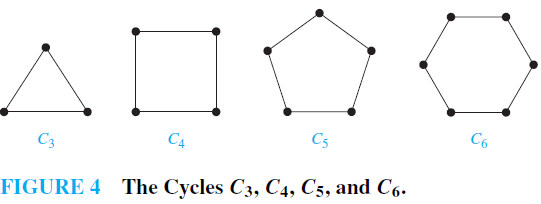
EXAMPLE 2 Cycles A cycle Cn, n ≥ 3, consists of n vertices v1, v2, . . . , vn and edges {v1, v2}, {v2, v3}, . . . , {vn−1, vn}, and {vn, v1}. The cycles C3, C4, C5, and C6 are displayed in Figure 4.

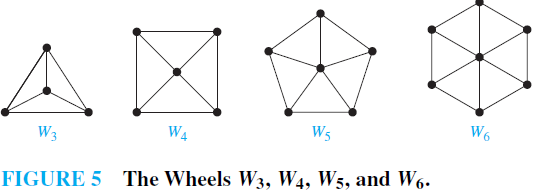
EXAMPLE 3 Wheels We obtain a wheel Wn when we add an additional vertex to a cycle Cn, for n ≥ 3, and connect this new vertex to each of the n vertices in Cn, by new edges. The wheels W3, W4, W5, and W6 are displayed in Figure 5.

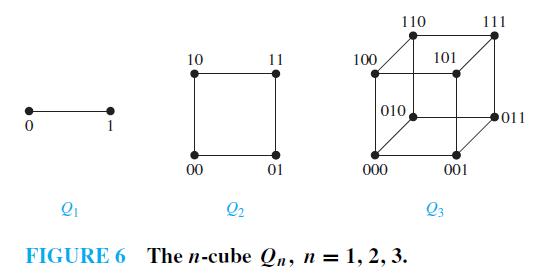
EXAMPLE 8: n-Cubes An n-dimensional hypercube, or n-cube, denoted byQn, is a graph that has vertices representing the 2n bit strings of length n. Two vertices are adjacent if and only if the bit strings that they represent differ in exactly one bit position.We display Q1, Q2, and Q3 in Figure 6. Note that you can construct the (n 1)-cube Qn 1 from the n-cube Qn by making two copies of Qn, prefacing the labels on the vertices with a 0 in one copy of Qn andwith a 1 in the other copy of Qn, and adding edges connecting two vertices that have labels differing only in the first bit. In Figure 6, Q3 is constructed from Q2 by drawing two copies of Q2 as the top and bottom faces of Q3, adding 0 at the beginning of the label of each vertex in the bottom face and 1 at the beginning of the label of each vertex in the top face. (Here, by face we mean a face of a cube in three-dimensional space. Think of drawing the graph Q3 in three-dimensional space with copies of Q2 as the top and bottom faces of a cube and then drawing the projection of the resulting depiction in the plane.)