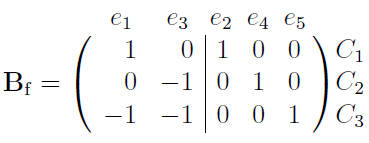Circuit Matrix: We consider a loopless graph G = (V,E) which contains circuits. We enumerate the circuits of G: C1, . . . ,Cℓ. The circuit matrix of G is an ℓ × m matrix B = (b_ij) where

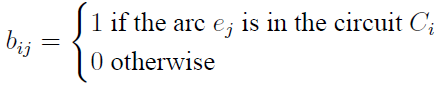
(as usual, E = {e1, . . . , em}).
The circuits in the digraph G are oriented, i.e. every circuit is given an arbitrary direction for the sake of defining the circuit matrix. After choosing the orientations, the circuit matrix of G is B = (b_ij) where

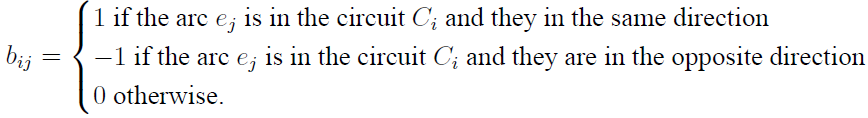
Example. For the directed graph

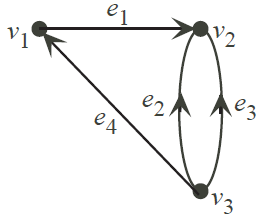
                                              the circuits are

 

 

 

 

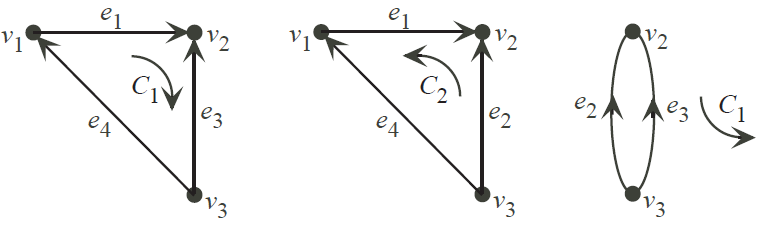
and the circuit matrix is

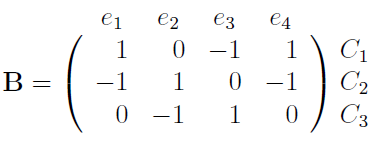
If the graph G is connected and contains at least one circuit, then it has a cospanning tree T∗ and the corresponding fundamental circuits. By choosing the corresponding rows of the circuit matrix B, we get an (m − n 1) ×m matrix B_f , called the fundamental circuit matrix. Similarly, a connected digraph G with at least one circuit has a fundamental circuit matrix: the direction of a fundamental circuit is the same as the direction of the corresponding link in T∗. When we rearrange the edges of G so that the links of T∗ come last and sort the fundamental circuits in the same order, the fundamental circuit matrix takes the form

where I_{m−n 1} is the identitymatrix withm−n 1 rows. The rank ofBf is thusm−n 1 = μ(G) and the rank of B is ≥ m − n 1.
Example. (Continuing from the previous example) We left out vertex v3 so we get a connected digraph (see p.34) and we chose the spanning tree

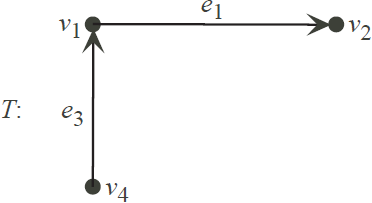
The fundamental circuits are

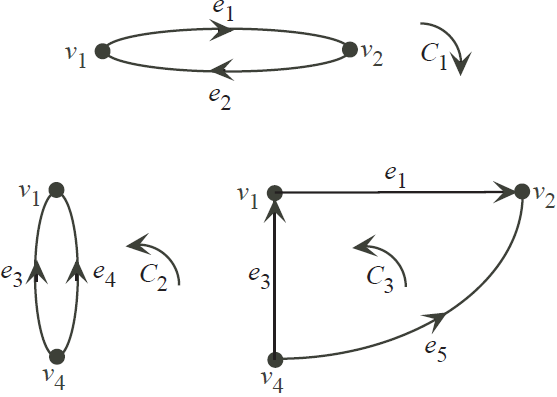
                                                         and