Euler’s Formula

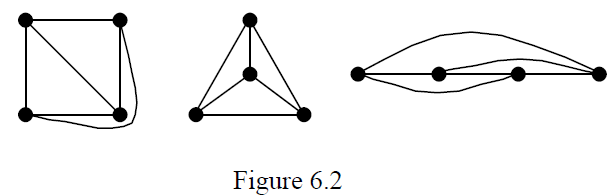
Euler’s formula for planar graphs . If n, m and f denote respectively the number of vertices, edges and faces in a plane drawing of a connected plane graph G then n– m f = 2. In figure 6.2 we have n= 4, m = 6 and f= 4 satisfying Euler’s formula.

Proof of Euler’s formula: A plane drawing of any connected planar graph G can be constructed by taking a spanning tree of G and adding edges to it,one at a time, until a plane drawing of G is obtained.

We prove Euler’s formula by showing that

(a) for any spanning tree of G, n– m f = 2 and
(b) adding an edge to the spanning tree does not change the value of n– m f.

Let T be any spanning tree of G. We may draw T in a plane without crossings. T has n vertices, n– 1 edges and 1 face (the infinite face). Thus n– m f = n – (n – 1) 1 = 2, so we have shown (a).

Now if we add an edge to T either it joins two different vertices, or it joins a vertex to itself (it is a loop). In either case it divides some face into two faces, so adding one face. Hence we have increased m, the number of edges, and f, the number of faces, by one each. The value of the expression n – m f is unchanged. We add more edges, one at a time, and at each addition the value of n– m f is unchanged. Hence we have shown (b) and so proved Euler’s theorem.

It is useful to be able to test a graph for planarity. There are a variety of algorithms for determining planarity, mostly quite complex. Here we will describe a simple test, the cycle method, which determines the planarity of a Hamiltonian graph.
First we identify a Hamiltonian cycle, C, in the graph. Now list the remaining edges of the graph, and then try to divide those edges into two disjoint sets A and B such that
A is a set of edges which can be drawn inside C without crossings and
B is a set of edges which can be drawn outside C without crossings.

Example: Determine whether the graph in figure 6.3 is planar.

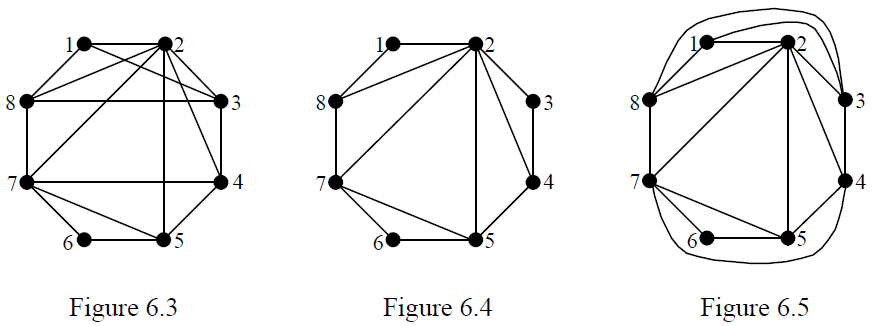
First find a Hamiltonian cycle. 123456781 will do. Draw a plane drawing of the cycle. The remaining edges are {24, 25, 27, 28, 31, 38, 47, 57}. Take the first edge, 24, and put it in set A. Take the second edge, 25, and put it in set A if compatible – it is so put it in set A. Consider the next edge, 27 – it is compatible with set A so add it to set A. At this point we have A = {24, 25, 27}, B = {}.

The next edge is 28 – it is compatible with set A so add it to set A (A = {24, 25, 27, 28}). The next edge is 31 which is not compatible with set A so put it in set B (B = {31}). The next edge is 38 which is not compatible with set A so put it in set B (B = {31, 38}). The next edge is 47 which is not compatible with set A so put it in set B (B = {31, 38, 47}). The next edge is 57 which is compatible with set A so put it in set A (A = {24, 25, 27, 28, 57}). Figure 6.4 shows the Hamiltonian cycle 123456781 and the edges in set A drawn inside the cycle. Now if we can add the edges from set B, all outside the cycle, without crossings then we have a plane drawing of the graph and it will be planar.

Figure 6.5 shows that the edges in set B can be drawn in that way so the graph is planar and figure 6.5 is a plane drawing.