Condensation, Reachability And Oreintable Graph

CONDENSATION: The condensation Gc of a digraph G is a digraph in which each strongly connected fragment is replaced by a vertex and all directed edges from one strongly connected component to another are replaced by a single directed edge.
The condensation of the digraph G in Fig. 8.10 is shown in Fig. 8.11.

Observations :
(i) The condensation of a strongly connected digraph is simply a vertex.
(ii) The condensation of a digraph has no directed circuit.

REACHABILITY: Given two vertices u and v of a digraph D, we say that v is reachable (or accessible) from u if there exists atleast one directed path in D from u to v.
For example, in the digraph shown in Fig. 8.1, the vertex v3 is reachable from the vertex v5, but v5 is not reachable from v3.

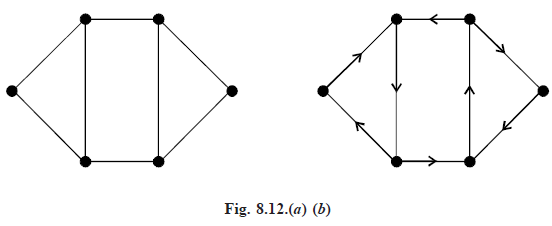
ORIENTABLE GRAPH: A graph G is said to be orientable if there exists a strongly connected digraph D for which G is the underlying graph.
For example, the graph is Fig. 8.12(a) is orientable, a strongly directed digraph for which this graph is the underlying graph is shown in Fig. 8.12(b).

ACCESSIBILITY: In a digraph a vertex b is said to be accessible (or reachable) from vertex a if there is a directed path from a to b. Clearly, a digraph G is strongly connected if and only if every vertex in G is accessible from every other vertex.