Decomposition Theorem

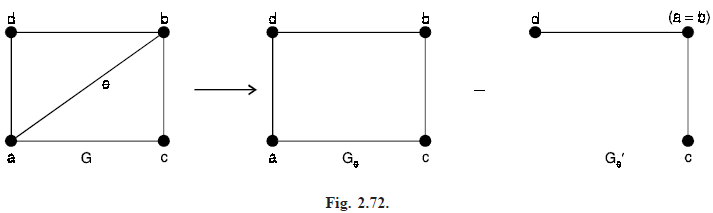
Decomposition theorem: If G = (V, E) is a connected graph and e = {a, b} ∈ E, then P(Ge, λ) = P(G, λ) P(Ge′, λ). Where Ge denotes the subgraph of G obtained by deleting e from G without removing vertices a and b.

i.e., Ge = G – e and Ge′ is a second subgraph of G obtained from Ge′ by colouring the vertices a and b.

Proof. Let e = {a, b}. The number of ways to properly color the vertices in Ge = G – e with (atmost) λ colours in P(Ge, λ).
Those colourings where end points a and b of e have different colours are proper colourings of G.
The colourings of Ge that are not proper colourigns of G occur when a and b have the same color. But each of these colourings corresponds with a proper colouring for Ge′. This partition of the P(Ge, λ) proper colourings of Ge into two disjoint subsets results in the equation
P(Ge, λ) = P(G, λ) P(Ge′, λ)

Problem. Using decomposition theorem find the chromatic polynomial and hence the chromatic number for the graph given below in Figure (2.73).

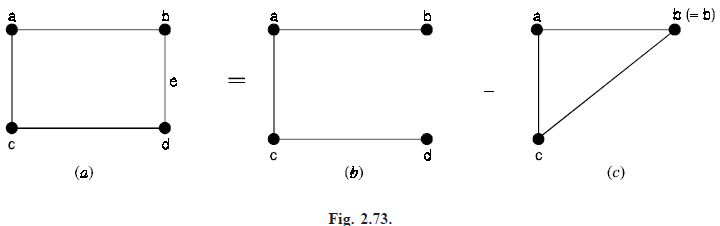
Solution. Deleting the edge e from G, we get G2 as shown in Figure (b). Then the chromatic polynomial of Ge is

P(Ge, λ) = λ(λ – 1)(λ – 2)

By colouring the endpoints of e, i.e., a and b, we get Ge′ as shown in Figure (c). Then the chromatic polynomial of Ge is

P(Ge′, λ) = λ(λ – 1)3.

Hence, by decomposition theorem, the chromatic polynomial of G is

P(G, λ) = λ(λ – 1)³ – λ(λ – 1)(λ – 2)
= λ(λ – 1) [(λ – 1)²(λ – 2)]
= λ(λ – 1) – (λ³ – 3λ 3) λ⁴
= 4λ³ 6λ – 3λ.